题目内容
已知函数 的导函数存在,则函数
的导函数存在,则函数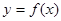 在一点的导数值为
在一点的导数值为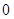 是函数
是函数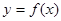 在这点取极值的( )
在这点取极值的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:因为函数 的导函数存在,所以当函数
的导函数存在,所以当函数 在
在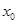 处取得极值时,必有
处取得极值时,必有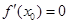 ;反过来若
;反过来若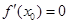 ,函数
,函数 在
在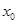 处不一定取得极值,如
处不一定取得极值,如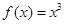 ,
,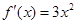 ,有
,有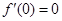 ,但由于
,但由于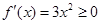 恒成立,所以
恒成立,所以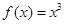 在
在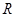 上单调递增,
上单调递增,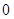 并不是函数
并不是函数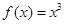 的极值点,故选B.
的极值点,故选B.
考点:1.函数的极值与导数;2.充分必要条件.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
若点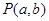 在函数
在函数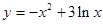 的图像上,点
的图像上,点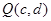 在函数
在函数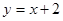 的图像上,则
的图像上,则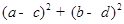 的最小值为( )
的最小值为( )
A.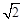 | B.2 | C.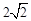 | D.8 |
若函数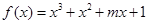 是R上的单调函数,则实数m的取值范围是( )
是R上的单调函数,则实数m的取值范围是( )
A.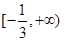 | B.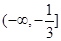 | C.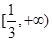 | D.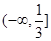  |
曲线 与
与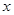 轴以及直线
轴以及直线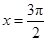 所围图形的面积为( )
所围图形的面积为( )
A.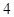 | B.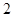 | C.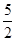 | D.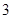 |
若函数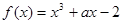 在区间
在区间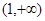 内是增函数,则实数
内是增函数,则实数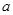 的取值范围是
的取值范围是
A.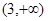 | B.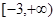 | C.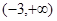 | D.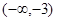 |
曲线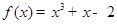 在
在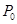 处的切线平行于直线
处的切线平行于直线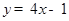 ,则
,则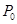 点的坐标为( )
点的坐标为( )
A.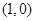 | B.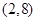 |
C.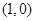 和 和 | D.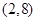 和 和 |
函数 的单调递减区间为( )
的单调递减区间为( )
A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边
长为( )
A.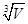 | B.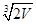 | C.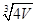 | D.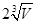 |
曲线y=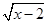 在点P(3,1)处的切线斜率为 ( ).
在点P(3,1)处的切线斜率为 ( ).
A.-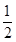 | B.0 | C.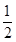 | D.1 |