题目内容
设函数
是
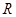上以5为周期的可导偶函数，则曲线
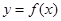在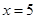
处的切线的斜率为
A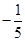． | B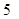． | C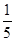． | D． |
D
解析试题分析：根据导数的定义，曲线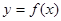
在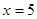
的切线的斜率为
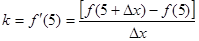，因为函数是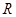上以5为周期的可导偶函数，所以
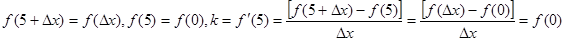因为是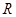上的偶函数，所以必有
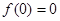，故曲线y=f(x)在x=5处的切线的斜率为0
考点：导数的定义，导数的几何意义，周期函数的性质，定义在R上的偶函数的性质
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知函数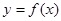
的图象关于原点对称，且当
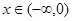时，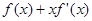
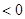成立，（其中
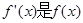的导函数），若
，
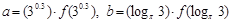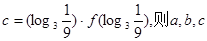的大小关系是（ ）
| A．a>b>C | B．c>b>a | C．c>a>b | D．a>c>b |
若函数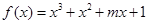
是R上的单调函数，则实数m的取值范围是（ ）
A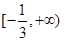． | B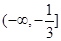． | C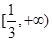． | D．  |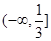
已知函数在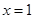
处的导数为1，则 
=
| A．3 | B． | C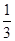． | D． |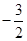
曲线
与
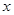轴以及直线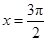
所围图形的面积为（ ）
A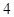． | B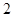． | C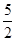． | D． |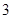
若函数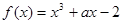
在区间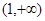
内是增函数，则实数
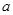的取值范围是
A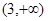． | B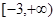． | C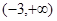． | D． |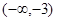
函数
的单调递减区间为（ ）
A．( 1,1） | B．(0,1] | C．[1,+∞) | D．(∞,-1)∪(0,1] |
已知函数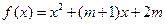
是偶函数，且
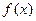在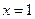
处的切线方程为
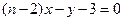，则常数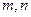
的积等于( )
| A．1 |
| B．2 |
| C．-3 |
| D．-4 |
函数y＝1＋3x－x3有 ( )．
| A．极小值－1，极大值1 | B．极小值－2，极大值3 |
| C．极小值－2，极大值2 | D．极小值－1，极大值3 |