题目内容
在平面直角坐标系xOy中,如图,已知椭圆C: 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.

(1)设直线AP、PB的斜率分别为k1,k2,求证:k1·k2为定值;
(2)求线段MN长的最小值;
(3)当点P运动时,以MN为直径的圆是否经过某定点?请证明你的结论.
【答案】
(1)k1·k2=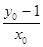 .
.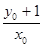 =
=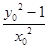 =-
=-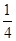 (2)MN长的最小值是4
(2)MN长的最小值是4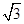 .
.
(3)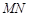 为直径的圆恒过定点
为直径的圆恒过定点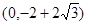 (或点
(或点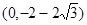 )
)
【解析】
试题分析:解:(1)由题设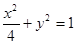 可知,点A(0,1),B(0,-1).
可知,点A(0,1),B(0,-1).
令P(x0,y0),则由题设可知x0≠0.
所以,直线AP的斜率k1=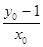 ,PB的斜率为k2=
,PB的斜率为k2=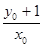 .
2分
.
2分
又点P在椭圆上,所以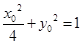 (x0≠0),从而有
(x0≠0),从而有
k1·k2=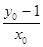 .
.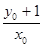 =
=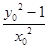 =-
=-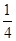 .
4分
.
4分
(2)由题设可以得到直线AP的方程为y-1=k1(x-0),直线PB的方程为
y-(-1)=k2(x-0).
由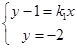 ,解得
,解得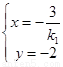 ;
;
由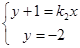 ,解得
,解得 .
.
所以,直线AP与直线l的交点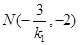 ,直线PB与直线l的交点
,直线PB与直线l的交点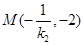 .
.
7分
于是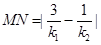 ,又k1·k2=-
,又k1·k2=-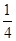 ,所以
,所以
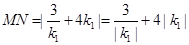 ≥2
≥2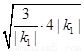 =4
=4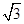 ,
,
等号成立的条件是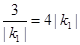 ,解得
,解得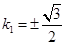 .
.
故线段MN长的最小值是4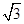 .
10分
.
10分
(3)设点Q(x,y)是以MN为直径的圆上的任意一点,则 =0,故有
=0,故有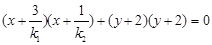 .
.
又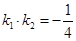 ,所以以MN为直径的圆的方程为
,所以以MN为直径的圆的方程为
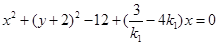 .
13分
.
13分
令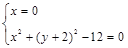 ,解得
,解得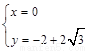 或
或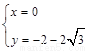 .
.
所以,以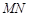 为直径的圆恒过定点
为直径的圆恒过定点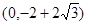 (或点
(或点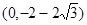 ).16分
).16分
注:写出一点的坐标即可得分.
考点:直线与椭圆的位置关系
点评:研究直线与圆的位置关系,以及直线与椭圆的位置关系,并结合向量的知识来处理,圆过定点的问题,利用数量积为零,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是