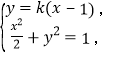Question

【题目】已知函数f(x)＝lnx＋2x－6。

(1)证明：函数f(x)在其定义域上是增函数；

(2)证明：函数f(x)有且只有一个零点；

(3)求这个零点所在的一个区间，使这个区间的长度不超过。

Answer 1

【答案】（1）见解析；（2）见解析；（3） .

【解析】

（1）直接根据函数单调性的定义，即可证明；

（2）由零点判定定理，即可证明；

（3）由（2）知，该零点在区间(2,3)上，从而利用二分法确定区间即可.

(1)证明：函数f(x)的定义域为(0，＋∞)，设0<x1<x2，则lnx1<lnx2, 2x1<2x2.

∴ lnx1＋2x1－6<lnx2＋2x2－6. ∴f(x1)<f(x2)．

∴ f(x)在(0，＋∞)上是增函数．

(2)证明：∵ f(2)＝ln2－2<0，f(3)＝ln3>0，

∴f(2)·f(3)<0. ∴ f(x)在(2,3)上至少有一个零点，

又由(1)可知f(x)在(0，＋∞)上是增函数，因此函数至多有一个根，

从而函数f(x)在(0，＋∞)上有且只有一个零点．

(3)解：由（2）可知f(x)的零点，

取，，

∴ 区间长度

取，，∴.

∴，区间长度，

∴即为符合条件的区间．