题目内容
已知{an}是由非负整数组成的无穷数列,该数列前n项的最大值记为An,第n项之后各项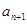 ,
,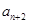 …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.
(1)若{an}为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意n∈N*,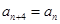 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值;
(2)设d为非负整数,证明:dn=-d(n=1,2,3…)的充分必要条件为{an}为公差为d的等差数列;
(3)证明:若a1=2,dn=1(n=1,2,3…),则{an}的项只能是1或2,且有无穷多项为1.
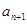 ,
,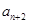 …的最小值记为Bn,dn=An-Bn.
…的最小值记为Bn,dn=An-Bn.(1)若{an}为2,1,4,3,2,1,4,3…,是一个周期为4的数列(即对任意n∈N*,
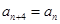 ),写出d1,d2,d3,d4的值;
),写出d1,d2,d3,d4的值;(2)设d为非负整数,证明:dn=-d(n=1,2,3…)的充分必要条件为{an}为公差为d的等差数列;
(3)证明:若a1=2,dn=1(n=1,2,3…),则{an}的项只能是1或2,且有无穷多项为1.
(1)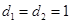 ,
,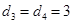 . (2)见解析 (3)见解析
. (2)见解析 (3)见解析
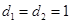 ,
,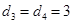 . (2)见解析 (3)见解析
. (2)见解析 (3)见解析充分利用题目所给信息进行反复推理论证.要证明充要条件,需要充分性和必要性两个方面叙述.
(1)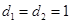 ,
,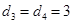 .
.
(2)充分性:因为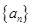 是公差为
是公差为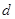 的等差数列,且
的等差数列,且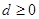 ,所以
,所以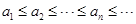 ,
,
因此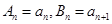 ,
,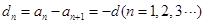 .
.
必要性:因为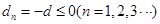 ,所以
,所以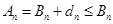 .
.
又因为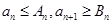 ,所以
,所以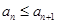 .
.
于是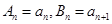 .
.
因此,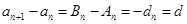 ,即
,即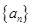 是公差为
是公差为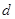 的等差数列.
的等差数列.
(3)因为a1=2,dn=1,所以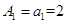 ,
,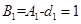 ,
,
故对任意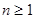 ,
,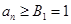 .
.
假设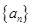
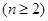 ,中存在大于2的项,
,中存在大于2的项,
设m为满足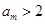 的的最小正整数,
的的最小正整数,
则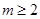 ,并且对任意
,并且对任意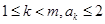 ,
,
又因为a1=2,所以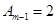 ,且
,且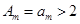 .
.
于是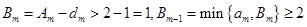 .
.
故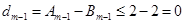 ,与
,与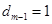 矛盾.
矛盾.
所以对于任意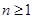 ,都有
,都有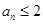 ,即非负整数数列
,即非负整数数列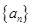 的各项只能为1或2,.
的各项只能为1或2,.
因为对任意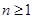 ,
,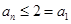 ,
,
所以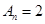 .
.
故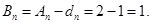
因此,对于任意正整数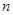 ,存在
,存在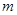 满足
满足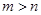 ,且
,且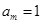 ,即数列{an}有无穷多项为1.
,即数列{an}有无穷多项为1.
【考点定位】本题考查了数列的周期性,等差数列.考查了推理论证能力和数据处理能力.试题难度较大,解答此题,需要非常强的分析问题和解决问题的能力.本题是一个信息题,考查了学生对知识的迁移能力.
(1)
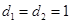 ,
,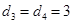 .
.(2)充分性:因为
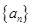 是公差为
是公差为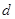 的等差数列,且
的等差数列,且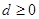 ,所以
,所以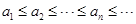 ,
,因此
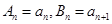 ,
,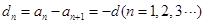 .
.必要性:因为
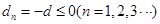 ,所以
,所以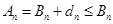 .
.又因为
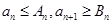 ,所以
,所以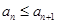 .
.于是
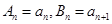 .
.因此,
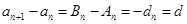 ,即
,即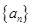 是公差为
是公差为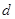 的等差数列.
的等差数列.(3)因为a1=2,dn=1,所以
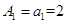 ,
,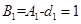 ,
,故对任意
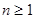 ,
,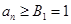 .
.假设
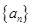
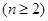 ,中存在大于2的项,
,中存在大于2的项,设m为满足
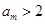 的的最小正整数,
的的最小正整数,则
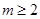 ,并且对任意
,并且对任意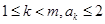 ,
,又因为a1=2,所以
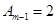 ,且
,且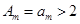 .
.于是
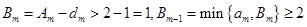 .
.故
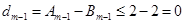 ,与
,与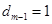 矛盾.
矛盾.所以对于任意
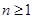 ,都有
,都有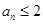 ,即非负整数数列
,即非负整数数列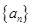 的各项只能为1或2,.
的各项只能为1或2,.因为对任意
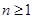 ,
,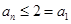 ,
,所以
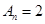 .
.故
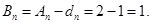
因此,对于任意正整数
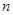 ,存在
,存在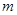 满足
满足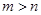 ,且
,且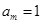 ,即数列{an}有无穷多项为1.
,即数列{an}有无穷多项为1.【考点定位】本题考查了数列的周期性,等差数列.考查了推理论证能力和数据处理能力.试题难度较大,解答此题,需要非常强的分析问题和解决问题的能力.本题是一个信息题,考查了学生对知识的迁移能力.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
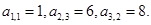
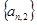 的通项公式;
的通项公式;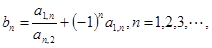 求数列
求数列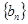 的前
的前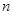 项和
项和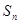 。
。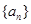 中,
中,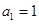 , 公比q="2" , 则其前n和
, 公比q="2" , 则其前n和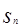 = .
= .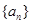 为等比数列, 其前
为等比数列, 其前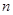 项和为
项和为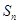 , 已知
, 已知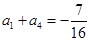 , 且对于任意的
, 且对于任意的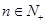 有
有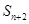 ,
, 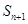 成等差;求数列
成等差;求数列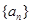 满足
满足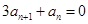 ,
,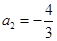 ,则
,则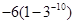
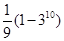
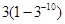
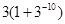
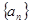 中,
中,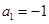 ,
,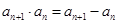 ,则数列通项
,则数列通项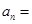 ___________
___________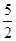 ,a1+a2+…+an=An2+Bn,n∈N+,其中A,B为常数,则AB=__________.
,a1+a2+…+an=An2+Bn,n∈N+,其中A,B为常数,则AB=__________.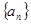 中,
中,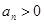 ,
,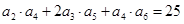 ,那么
,那么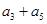 等于
等于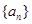 的各项均为正数,
的各项均为正数,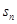 为其前
为其前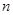 项和,对于任意的
项和,对于任意的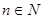 ,满足关系式
,满足关系式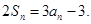
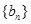 的通项公式是
的通项公式是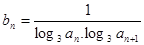 ,前
,前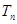 ,求证:对于任意的正整数n,总有
,求证:对于任意的正整数n,总有