题目内容
【题目】已知函数f(x)=x|x﹣2|.
(1)作出函数f(x)=x|x﹣2|的大致图象;
(2)若方程f(x)﹣k=0有三个解,求实数k的取值范围.
(3)若x∈(0,m](m>0),求函数y=f(x)的最大值.
【答案】
(1)解:函数f(x)=x|x﹣2|= 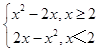 ,
,
由分段函数的画法,可得如图
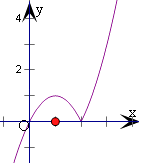
(2)解:若方程f(x)﹣k=0有三个解,即函数f(x)图象与直线y=k有三个交点,
由图可得,当0<k<1时,有三个交点,即方程f(x)﹣k=0有三个解
(3)解:当0<m≤1时,f(x)在(0,m]递增,f(m)取得最大值,且为2m﹣m2;
由x2﹣2x=1,解得x=1+ ![]() (1﹣
(1﹣ ![]() 舍去),
舍去),
当1<m≤1+ ![]() 时,由f(x)的图象可得f(1)取得最大值1;
时,由f(x)的图象可得f(1)取得最大值1;
当m>1+ ![]() 时,由f(x)的图象可得f(m)取得最大值m2﹣2m.
时,由f(x)的图象可得f(m)取得最大值m2﹣2m.
综上可得,当0<m≤1时,f(x)的最大值为2m﹣m2;
当1<m≤1+ ![]() 时,f(x)的最大值为1;
时,f(x)的最大值为1;
当m>1+ ![]() 时,f(x)的最大值为m2﹣2m.
时,f(x)的最大值为m2﹣2m.
【解析】(1)写出f(x)的分段形式,画出图象;(2)由题意可得,函数f(x)图象与直线y=k有三个交点,通过平移直线y=k,即可得到k 范围;(3)对m讨论,分当0<m≤1时,当1<m≤1+ ![]() 时,当m>1+
时,当m>1+ ![]() 时,三种情况,通过图象和单调性,即可得到最大值.
时,三种情况,通过图象和单调性,即可得到最大值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目