题目内容

精英家教网A．（不等式选做题）不等式|
x+2
x+1
|≤1的实数解集为
 
．
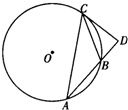
B．（几何证明选做题）如图，在△ABC中，AB=AC，以BC为直径的半圆O与边AB相交于点D，切线DE⊥AC，垂足为点E．则
AE
CE
=
 
．
C．（坐标系与参数方程选做题）若△ABC的底边BC=10，∠B=2∠A，以B点为极点，BC 为极轴，则顶点A 的极坐标方程为
 
．
分析：可直接转化为
|x+2|≤|x+1
x+1≠0
，两边平方去绝对值解决，注意|x+1|≠0
解答：解：不等式|
x+2
x+1
|≤1 可化为：
|x+2|≤|x+1
x+1≠0
，
(x+2)2≤(x+1)2
x+1≠0
?x≤-
3
2
．
∴解集为 {x|x≤-
3
2
}．
故答案为：{x|x≤-
3
2
}．
点评：本题考查解绝对值不等式，解绝对值不等式的关键是去绝对值，常用方法有：分段讨论、平方、利用绝对值的集合意义等．
练习册系列答案
相关题目
精英家教网A．（不等式选做题）
函数f（x）=x2-x-a2+a+1对于任一实数x，均有f（x）≥0．则实数a满足的条件是
 
．
B．（几何证明选做题）
如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=2
3
，AB=BC=4，则AC的长为
 
．
C．（坐标系与参数方程选做题）
在极坐标系中，曲线ρ=4cos(θ-
π
3
)上任意两点间的距离的最大值为
 
．
精英家教网A．（不等式选做题）不等式|3x-6|-|x-4|＞2x的解集为
 
．

B．（几何证明选做题）如图，直线PC与圆O相切于点C，割线PAB经过圆心O，
弦CD⊥AB于点E，PC=4，PB=8，则CE=
 
．
C．（坐标系与参数方程选做题）在极坐标系中，圆ρ=4cosθ的圆心到直线ρsin(θ+
π
4
)=2
2
的距离为
 
．
（请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）若不等式|x+1|+|x-2|≥a对任意x∈R恒成立，则a的取值范围是
 
．
B．（几何证明选做题）如图，∠B=∠D，AE⊥BC，∠ACD=90°，且AB=6，AC=4，AD=12，则AE=
 
．
精英家教网
C．（坐标系与参数方程选做题）直角坐标系xoy中，以原点为极点，x轴的正半轴为极轴建极坐标系，设点A，B分别在曲线C1：
x=3+cosθ
y=sinθ
 （θ为参数）和曲线C2：p=1上，则|AB|的最小值为
 
．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）不等式|x-5|+|x+3|≥10的解集是
{x|x≥6或x≤-4}
{x|x≥6或x≤-4}
．
B．（坐标系与参数方程选做题）在极坐标系中，圆ρ=-2sinθ的圆心的极坐标是
（1，
3π
2
）
（1，
3π
2
）
．
C．（几何证明选做题）如图，已知圆中两条弦AB与CD相交于点F，E是AB延长线上一点，且DF=CF=2
2
，BE=1，BF=2，若CE与圆相切，则线段CE的长为
7
7
．
选做题：（考生注意：请在下列三题中任选一题作答，如果多做，则按所做第一题评分）
A．（不等式选做题）不等式
x+5
(x-1)2
≥2的解集是
[-
1
2
，1）∪（1，3]
[-
1
2
，1）∪（1，3]
．
B．（几何证明选做题） 如图，⊙O的直径AB=6cm，P是延长线上的一点，过点P作⊙O的切线，切点为C，连接AC，若∠CAP=30°，则PC=
3
3
3
3
．
C．（坐标系与参数方程选做题）已知直线x+2y-4=0与
x=2-3cosθ
y=1+3sinθ
（θ为参数）相交于A、B两点，则|AB|=
6
6
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网