题目内容
A.(不等式选做题)
函数f(x)=x
2-x-a
2+a+1对于任一实数x,均有f(x)≥0.则实数a满足的条件是
.
B.(几何证明选做题)
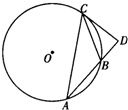
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,
CD=2,AB=BC=4,则AC的长为
.
C.(坐标系与参数方程选做题)
在极坐标系中,曲线
ρ=4cos(θ-)上任意两点间的距离的最大值为
.
分析:A 由函数f(x)=x2-x-a2+a+1对于任一实数x,均有f(x)≥0,故判别式△=4a2-4a-3≤0,解出a 的范围.
B 由切线长定理求得DB=2,在△ABC 和△ACD 中,分别使用余弦理,解方程组求得 AC 的长.
C 把极坐标方程化为普通方程,可得曲线表示一个圆,故曲线上任意两点间的距离最大值为圆的直径.
解答:解:A,∵函数f(x)=x
2-x-a
2+a+1对于任一实数x,均有f(x)≥0.∴△=4a
2-4a-3≤0,
解得-
≤a≤
.
B,由圆的切割线定理得 DC
2=DB×DA,∴12=DB×(4+DB ),DB=2,DA=2+4=6,
设 AC=x,∠CAB=θ,在△ABC 和△ACD 中,分别使用余弦理得:
16=x
2+16-2x•4cosθ,12=x
2+36-2x•6cosθ,消去θ,解得 x=4
.
C,曲线
ρ=4cos(θ-) 即 ρ=2cosθ+
sinθ,∴x
2+y
2=2x+
y,
(x-1)2+(y-)2=
,表示圆心在(1,
),半径等于
的圆.圆上任意两点间的距离最大
为直径
.
综上,故答案为:-
≤a≤
;4
;
.
点评:本题考查把极坐标方程化为普通方程,函数的恒成立问题,圆的切割线定理的应用.
练习册系列答案
相关题目
 A.(不等式选做题)
A.(不等式选做题)
 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)