题目内容
 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
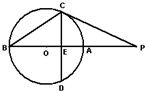
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为B.(几何证明选做题)如图,直线PC与圆O相切于点C,割线PAB经过圆心O,
弦CD⊥AB于点E,PC=4,PB=8,则CE=
C.(坐标系与参数方程选做题)在极坐标系中,圆ρ=4cosθ的圆心到直线ρsin(θ+
| π |
| 4 |
| 2 |
分析:A把原不等式转化为与之等价的不等式组来解,原不等式的解集是这3个不等式组阶级的并集,
B由切割线定理求得PA,即可求得半径,由由Rt△COE∽Rt△POC,对应边成比列求出CE,
C把极坐标方程化为直角坐标方程,用点到直线的距离公式求出圆心到直线的距离.
B由切割线定理求得PA,即可求得半径,由由Rt△COE∽Rt△POC,对应边成比列求出CE,
C把极坐标方程化为直角坐标方程,用点到直线的距离公式求出圆心到直线的距离.
解答:解:A∵不等式|3x-6|-|x-4|>2x,∴
①,或
②,
③. 解①得 x无解; 解②得 x无解; 解③得 x<
,
故原不等式的解集为 {x|x<
}.
B 由切割线定理得 PC2=PA•PB,16=PA×8,∴PA=2,
直径AB=PB-PA=8-2=6,半径等于3;
由Rt△COE∽Rt△POC得
=
,
=
,CE=
.
C 圆ρ=4cosθ的直角坐标方程为 x2+y2=4x,表示圆心为(2,0),半径等于2的圆.
直线ρsin(θ+
)=2
即
ρcosθ+
sinθ=2
,x+y=4,
故圆心到直线的距离等于
=
.
故答案为:A {x|x<
},B
,C
.
|
|
|
| 1 |
| 2 |
故原不等式的解集为 {x|x<
| 1 |
| 2 |
B 由切割线定理得 PC2=PA•PB,16=PA×8,∴PA=2,
直径AB=PB-PA=8-2=6,半径等于3;
由Rt△COE∽Rt△POC得
| CE |
| PC |
| CO |
| PO |
| CE |
| 4 |
| 3 |
| 3+2 |
| 12 |
| 5 |
C 圆ρ=4cosθ的直角坐标方程为 x2+y2=4x,表示圆心为(2,0),半径等于2的圆.
直线ρsin(θ+
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
故圆心到直线的距离等于
| |2+0-4| | ||
|
| 2 |
故答案为:A {x|x<
| 1 |
| 2 |
| 12 |
| 5 |
| 2 |
点评:本题考查绝对值不等式的解法,圆的切割线定理,把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,体现了分类讨论、以及转化的数学思想.

练习册系列答案
相关题目
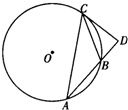 A.(不等式选做题)
A.(不等式选做题)
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)