题目内容
 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)A.(不等式选做题)不等式
| x+5 |
| (x-1)2 |
[-
,1)∪(1,3]
| 1 |
| 2 |
[-
,1)∪(1,3]
.| 1 |
| 2 |
B.(几何证明选做题) 如图,⊙O的直径AB=6cm,P是延长线上的一点,过点P作⊙O的切线,切点为C,连接AC,若∠CAP=30°,则PC=
3
| 3 |
3
.| 3 |
C.(坐标系与参数方程选做题)已知直线x+2y-4=0与
|
6
6
.分析:(A)由不等式
≥2 可得2x2-5x-3≤0,解此一元二次不等式,求得解集.
(B)在圆中线段利用由切线定理求得∠OCP=Rt∠,进而利用直角三角形PCO中的线段,结合解直角三角形求得PC即可.
(C)把参数方程消去参数化为直角坐标方程,表示以(2,1)为圆心,半径等于3的圆,圆心到直线的距离等于0可得AB为直径,从而得到AB的值.
| x+5 |
| (x-1)2 |
(B)在圆中线段利用由切线定理求得∠OCP=Rt∠,进而利用直角三角形PCO中的线段,结合解直角三角形求得PC即可.
(C)把参数方程消去参数化为直角坐标方程,表示以(2,1)为圆心,半径等于3的圆,圆心到直线的距离等于0可得AB为直径,从而得到AB的值.
解答:解:(A)由不等式
≥2 可得2x2-5x-3≤0,解得 x∈[-
,1)∪(1,3],
故答案为[-
,1)∪(1,3].
(B) 连接OC,由于 PC是⊙O的切线,∴∠OCP=90°,∵∠CPA=30°,∴OC=
=3,由tan30°=
,求得PC=3
.
故答案为 3
.
(C)把
消去参数化为直角坐标方程为 (x-2)2+(y-1)2=9,表示以(2,1)为圆心,半径等于3的圆.
圆心到直线的距离等于
=0,故AB为直径,故AB=6,
故答案为 6.
| x+5 |
| (x-1)2 |
| 1 |
| 2 |
故答案为[-
| 1 |
| 2 |
(B) 连接OC,由于 PC是⊙O的切线,∴∠OCP=90°,∵∠CPA=30°,∴OC=
| AB |
| 2 |
| 3 |
| PC |
| 3 |
故答案为 3
| 3 |
(C)把
|
圆心到直线的距离等于
| |2+2-4| | ||
|
故答案为 6.
点评:此题考查的是分式不等式的解法,直角三角形的性质、与圆有关的比例线段以及切线定理,把参数方程化为普通方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,
属于基础题.
属于基础题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
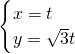 (t为参数)的距离是________.
(t为参数)的距离是________. 的解集是 .
的解集是 .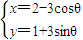 (θ为参数)相交于A、B两点,则|AB|= .
(θ为参数)相交于A、B两点,则|AB|= .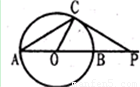
 (t为参数)的距离是 .
(t为参数)的距离是 .