题目内容
已知函数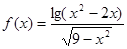 的定义域为
的定义域为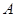 ,
,
(1)求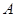 ;
;
(2)若 ,且
,且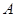 是
是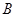 的真子集,求实数
的真子集,求实数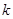 的取值范围.
的取值范围.
(1)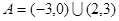 ;(2)
;(2)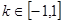 .
.
解析试题分析:(1) 本小题求函数的定义域,主要涉及到对数的真数大于零、二次根号下非负、分式的分母不等于零,联立不等式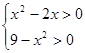 解之即可;
解之即可;
(2) 本小题考查集合之间的关系,可以从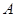 是
是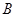 的真子集来考虑参数需要满足的条件,也可以把问题转化为恒成立的问题来求解.
的真子集来考虑参数需要满足的条件,也可以把问题转化为恒成立的问题来求解.
试题解析:(1)由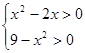 , 2分
, 2分
解得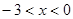 或
或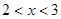 ,
,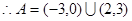 4分
4分
(2)法一: 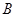 中
中 6分
6分
1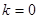 时,
时,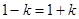 ,此时
,此时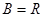 ,符合题意; 8分
,符合题意; 8分
2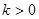 时,
时,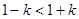 ,此时
,此时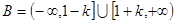 ,由
,由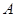 是
是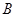 的
的
真子集得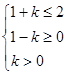
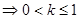 , 10分
, 10分
3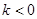 时,
时,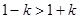 ,此时
,此时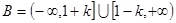 ,由
,由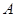 是
是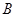 的
的
真子集得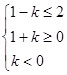
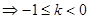 , 12分
, 12分
综上得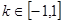 14分
14分
法二:因为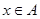 时总有
时总有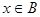 ,
,
所以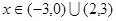 时总有
时总有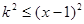 8分
8分
所以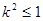 ,
,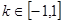 ; 12分
; 12分
此时,显然有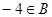 但
但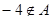 ,所以
,所以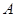 是
是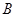 的真子集,综上得
的真子集,综上得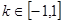 14分
14分
考点:1.函数定义域;2.集合的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的二次方程
的二次方程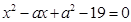 和
和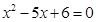 的解集分别是集合
的解集分别是集合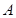 和
和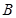 ,若
,若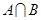 为单元素集,求
为单元素集,求 的值.
的值. 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 ,已知
,已知 :
: ;
; :
: 满足
满足 ,且若
,且若 的取值范围.
的取值范围.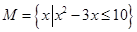 ,
,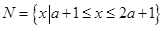 .
.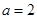 ,求
,求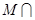 (
(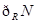 );
);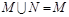 ,求实数
,求实数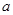 的取值范围.
的取值范围.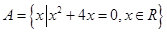 ,
,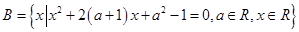 ,若
,若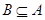 ,求实数
,求实数 的取值范围.
的取值范围.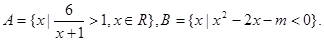
 =3时,求
=3时,求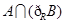 ;
;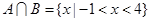 ,求实数
,求实数 ,集合
,集合 =
= ,
,  求:
求:
 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定 .
. (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.  ,
,
 =1时,求
=1时,求
 ,求
,求