题目内容
定义平面向量之间的一种运算“☉”如下:对任意的a=(m,n),b=(p,q),令a☉b=mq-np.下面说法错误的是( )
| A.若a与b共线,则a☉b=0 |
| B.a☉b=b☉a |
| C.对任意的λ∈R,有(λa)☉b=λ(a☉b) |
| D.(a☉b)2+(a·b)2=|a|2|b|2 |
B
若a与b共线,有a☉b=mq-np=0,故选项A正确;
∵b☉a=pn-qm,
而a☉b=mq-np,
∴a☉b≠b☉a,故选项B错误;
∵(λa)☉b=λmq-λnp=λ(mq-np)=λ(a☉b),故选项C正确;
∵(a☉b)2+(a·b)2=(mq-np)2+(mp+nq)2=(m2+n2)(p2+q2)=|a|2|b|2,故选项D正确.
∵b☉a=pn-qm,
而a☉b=mq-np,
∴a☉b≠b☉a,故选项B错误;
∵(λa)☉b=λmq-λnp=λ(mq-np)=λ(a☉b),故选项C正确;
∵(a☉b)2+(a·b)2=(mq-np)2+(mp+nq)2=(m2+n2)(p2+q2)=|a|2|b|2,故选项D正确.

练习册系列答案
相关题目
 ,其中
,其中 表示不小于
表示不小于 的最小整数,如
的最小整数,如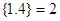 ,
,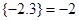 .当
.当 (
( )时,函数
)时,函数 的值域为
的值域为 ,记集合
,记集合 ,则
,则 ________________.
________________.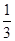 [k(k+1)(k+2)-(k-1)k(k+1)],
[k(k+1)(k+2)-(k-1)k(k+1)], a;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .
a;类比到空间,设P是棱长为a的空间正四面体ABCD内的一点,则P点到四个面的距离之和h1+h2+h3+h4= .

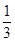 +
+ =1;
=1;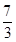 +
+ +
+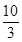 +
+ =12;
=12;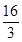 +
+ +
+ +
+ +
+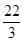 +
+ =39;
=39; +
+ +
+ +
+ +…+
+…+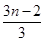 +
+ =________(最后结果用m,n表示).
=________(最后结果用m,n表示).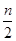 );如果n是奇数,则将它乘3加1(即
);如果n是奇数,则将它乘3加1(即 ),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:
),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究: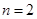 ,则按照上述规则施行变换后的第8项为 .
,则按照上述规则施行变换后的第8项为 . (首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则
(首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则 则ak+1=( ).
则ak+1=( ).
 -
-