题目内容
如图,已知圆⊙O1与圆⊙O2外切于点P,过点P的直线交圆⊙O1于A,交圆⊙O2于B,AC为圆⊙O1直径,BD与⊙O2相切于B,交AC延长线于D.

(Ⅰ)求证:
(Ⅱ)若BC、PD相交于点M,则

(Ⅰ)求证:

(Ⅱ)若BC、PD相交于点M,则

见详解
试题分析:(Ⅰ)根据切线的性质证明;(Ⅱ)由P、B、D、C四点共圆,又易证
 ,即根据三角形相似得出相似比.
,即根据三角形相似得出相似比.试题解析:
证明:(Ⅰ)如图,过点P作两圆公切线交BD于T,

连接PC ,∵AC为直径,
 ,
, ,
, ,
,又BD与⊙O2相切于B,
PT为两圆公切线,
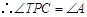 ,
, ,
, ,
, ,
,故
 . (5分)
. (5分)(Ⅱ) 由(Ⅰ)易证
 ∽
∽ ,
,∴
 又由(Ⅰ)知∠ACP=∠DBP,
又由(Ⅰ)知∠ACP=∠DBP,∴P、B、D、C四点共圆,又易证
 ,
,
∴

∴
 . (10分)
. (10分)
练习册系列答案
相关题目
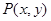 是圆
是圆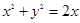 上的点
上的点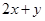 的取值范围.
的取值范围.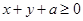 恒成立,求实数
恒成立,求实数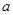 的取值范围.
的取值范围. 的圆
的圆 中,
中, ,
, 为
为 的中点,
的中点,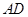 的延长线交圆
的延长线交圆 ,则线段
,则线段 的长为 .
的长为 .
 、
、 是半径为
是半径为 的圆
的圆 的两条弦,它们相交于
的两条弦,它们相交于 ,且
,且 ,
, ,则
,则 ____.
____.
 :
: +
+ =1,圆
=1,圆 与圆
与圆 对称,则圆
对称,则圆 +
+ =1
=1 +
+ =1
=1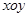 中,圆
中,圆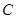 的方程为
的方程为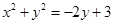 ,直线
,直线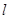 过点
过点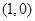 且与直线
且与直线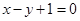 垂直.若直线
垂直.若直线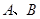 两点,则
两点,则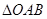 的面积为( )
的面积为( )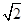
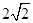
 中,直线
中,直线 与圆
与圆 相交于
相交于 两点,则弦
两点,则弦 的长等于( )
的长等于( )


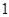
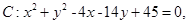 及点
及点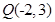 .
.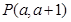 在圆上,求线段
在圆上,求线段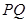 的长及直线
的长及直线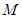 为圆
为圆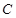 上任一点,求
上任一点,求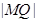 的最大值和最小值;
的最大值和最小值;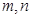 满足
满足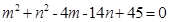 ,求
,求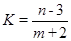 的最大值和最小值.
的最大值和最小值.