题目内容
某公司计划2013年在甲、乙两个电视台做总时间不超过300分钟的广告,广告总费用不超过9万元,甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟,规定甲、乙两个电视台为该公司所做的每分钟广告能给公司带来的收益分别为0.3万元和0.2万元.问该公司如何分配在甲、乙两个电视台的广告时间,才能使公司的收益最大,最大收益是多少万元?
该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.
设公司在甲电视台和乙电视台做广告的时间分别为x分钟和y分钟,总收益为z元.由题意,得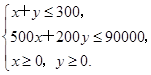 目标函数为z=3000x+2000y.
目标函数为z=3000x+2000y.
二元一次不等式组等价于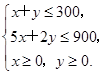
作出二元一次不等式组所表示的平面区域,即可行域.
作直线l:3000x+2000y=0,即3x+2y=0.
联立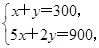 解得x=100,y=200.记点M的坐标为(100,200).
解得x=100,y=200.记点M的坐标为(100,200).
平移直线l,易知,当直线l过M点时,目标函数取得最大值.
∴zmax=3000x+2000y=700000(元).
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.
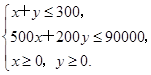 目标函数为z=3000x+2000y.
目标函数为z=3000x+2000y.二元一次不等式组等价于
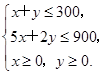
作出二元一次不等式组所表示的平面区域,即可行域.
作直线l:3000x+2000y=0,即3x+2y=0.
联立
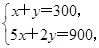 解得x=100,y=200.记点M的坐标为(100,200).
解得x=100,y=200.记点M的坐标为(100,200).平移直线l,易知,当直线l过M点时,目标函数取得最大值.
∴zmax=3000x+2000y=700000(元).
答:该公司在甲电视台做100分钟广告,在乙电视台做200分钟广告,公司的收益最大,最大收益是70万元.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 ”是“关于
”是“关于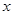 、
、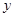 的不等式组
的不等式组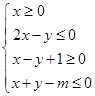 表示的平面区域为三角形”的( )
表示的平面区域为三角形”的( ) 其中实数
其中实数 满足
满足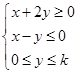 ,若
,若 的最大值为
的最大值为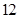 ,则
,则

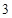

 表示的平面区域的公共点有______个.
表示的平面区域的公共点有______个.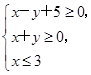 表示的平面区域.
表示的平面区域. 表示的平面区域内到直线y=2x-4的距离最远的点的坐标为________.
表示的平面区域内到直线y=2x-4的距离最远的点的坐标为________.
 则2x-y+3的最小值是( )
则2x-y+3的最小值是( )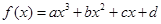 的图像如图所示,则
的图像如图所示,则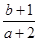 的取值范围是( )
的取值范围是( )