题目内容
18.在极坐标系中,设圆C1:ρ=4cosθ 与直线l:θ=$\frac{π}{4}$ (ρ∈R)交于A,B两点.(Ⅰ)求以AB为直径的圆C2的极坐标方程;
(Ⅱ)在圆C1任取一点M,在圆C2上任取一点N,求|MN|的最大值.
分析 (Ⅰ) 圆C1:ρ=4cosθ 化为ρ2=4ρcosθ,利用$\left\{\begin{array}{l}{{ρ}^{2}={x}^{2}+{y}^{2}}\\{x=ρcosθ}\end{array}\right.$即可得出圆C1的直角坐标方程.由直线l:θ=$\frac{π}{4}$ (ρ∈R)可得直线l的倾斜角为$\frac{π}{4}$,又经过原点,即可得出直角坐标方程.联立解得A,B坐标,即可得出圆的方程.再将其化为极坐标方程即可.
(II)利用|MN|max=|C1C2|+r1+r2即可得出.
解答 解:(Ⅰ) 以极点为坐标原点,极轴为x轴的正半轴,建立直角坐标系,则由题意得
圆C1:ρ=4cosθ 化为ρ2=4ρcosθ,∴圆C1的直角坐标方程 x2+y2-4x=0.
直线l的直角坐标方程 y=x.
由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-4x=0}\\{y=x}\end{array}\right.$,解得$\left\{\begin{array}{l}x=0\\ y=0\end{array}$或 $\left\{\begin{array}{l}x=2\\ y=2\end{array}$.
∴A(0,0),B(2,2).
从而圆C2的直角坐标方程为(x-1)2+(y-1)2=2,即x2+y2=2x+2y.
将其化为极坐标方程为:ρ2=2ρcosθ+2ρsinθ.
(Ⅱ)∵${C_1}(2,0),{r_1}=2,{C_2}(1,1),{r_2}=\sqrt{2}$,
∴|MN|max=|C1C2|+r1+r2=$\sqrt{2}$+2+$\sqrt{2}$=2$\sqrt{2}$+2.
点评 本题考查了参数方程化为直角坐标方程、极坐标方程与直角坐标方程互化、两圆的位置关系、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案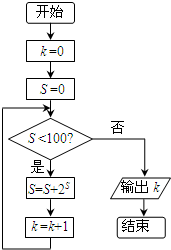
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
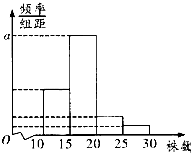 某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:
某单位组织职工开展构建绿色家园活动,在今年3月份参加义务植树活动的职工中,随机抽取M名职工为样本,得到这些职工植树的株数,根据此数据作出了频数与频率统计表和频率分布直方图如图:(1)求出表中M,p及图中a的值;
(2)单位决定对参加植树的职工进行表彰,对植树株数在[25,30)区间的职工发放价值800元的奖品,对植树株数在[20,25)区间的职工发放价值600元的奖品,对植树株数在[15,20)区间的职工发放价值400元的奖品,对植树株数在[10,15)区间的职工发放价值200元的奖品,在所取样本中,任意取出2人,并设X为此二人所获得奖品价值之差的绝对值,求X的分布列与数学期望E(X).
| 分组 | 频数 | 频率 |
| [10,15) | 5 | 0.25 |
| [15,20) | 12 | n |
| [20,25) | m | p |
| [25,30) | 1 | 0.05 |
| 合计 | M | 1 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |