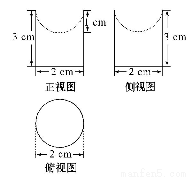
题目内容
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.

求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
见解析
【解析】建立空间直角坐标系.(1)可证明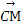 与平面PAD的法向量垂直;也可将
与平面PAD的法向量垂直;也可将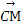 分解为平面PAD内的两个向量的线性组合,利用共面向量定理证明.
分解为平面PAD内的两个向量的线性组合,利用共面向量定理证明.
(2)取AP中点E,利用向量证明BE⊥平面PAD即可.
【证明】由题意可知:
以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴建立如图所示的空间直角坐标系Cxyz.
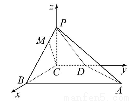
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABCD所成的角,
∴∠PBC=30°.
∵PC=2,∴BC=2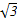 ,PB=4.
,PB=4.
∴D(0,1,0),B(2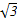 ,0,0),
,0,0),
A(2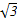 ,4,0),P(0,0,2),M(
,4,0),P(0,0,2),M( ,0,
,0,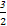 ),
),
∴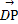 =(0,-1,2),
=(0,-1,2),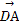 =(2
=(2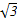 ,3,0),
,3,0),
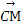 =(
=( ,0,
,0,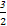 ).
).
(1)方法一:令n=(x,y,z)为平面PAD的一个法向量,则
即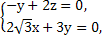 ∴
∴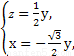
令y=2,得n=(-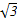 ,2,1).
,2,1).
∵n·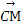 =-
=-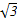 ×
× +2×0+1×
+2×0+1×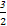 =0,
=0,
∴n⊥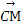 .又CM?平面PAD,
.又CM?平面PAD,
∴CM∥平面PAD.
方法二:∵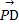 =(0,1,-2),
=(0,1,-2),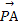 =(2
=(2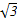 ,4,-2),
,4,-2),
假设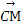 ∥平面PAD,
∥平面PAD,
则存在x0,y0使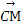 =x0
=x0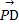 +y0
+y0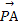 ,则
,则
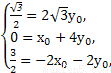 方程组的解为
方程组的解为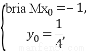
∴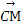 =-
=-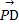 +
+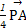 .
.
由共面向量定理知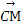 与
与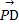 ,
,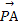 共面,故假设成立.
共面,故假设成立.
又∵CM?平面PAD,
∴CM∥平面PAD.
(2)取AP的中点E,连接BE,则E(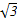 ,2,1),
,2,1),
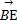 =(-
=(-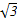 ,2,1).
,2,1).
易知PB=AB,∴BE⊥PA.
又∵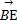 ·
·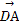 =(-
=(-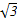 ,2,1)·(2
,2,1)·(2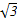 ,3,0)=0,
,3,0)=0,
∴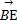 ⊥
⊥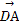 ,∴BE⊥DA.又PA∩DA=A,
,∴BE⊥DA.又PA∩DA=A,
∴BE⊥平面PAD.
又∵BE?平面PAB,
∴平面PAB⊥平面PAD.

练习册系列答案
相关题目