题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,且 ,则角A的大小为( )
,则角A的大小为( )
A.  B.
B.  C.
C.  D.
D. 
C
解析试题分析:利用正弦定理化边为角,再切化弦,利用和角的公式,化简求解角A.
根据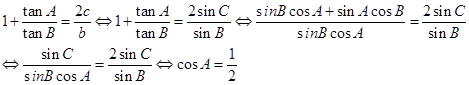
由此得到角A为 ,选C.
,选C.
考点:解三角形的运用
点评:本试题考查了正弦定理的运用,考查两角和差的正弦公式,解题的关键是利用正弦定理化边为角。

练习册系列答案
相关题目
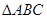 中,若
中,若 ,
, ,
, ,则
,则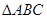 的面积为( )
的面积为( )
A. | B. | C. 或 或 | D. 或 或 |
等腰三角形一腰上的高是 ,这条高与底边的夹角为
,这条高与底边的夹角为 ,则底边长=( )
,则底边长=( )
| A.2 | B. | C.3 | D. |
在 的对边分别为
的对边分别为 ,若
,若 成等差数列则
成等差数列则 ( )
( )
A. | B. | C. | D. |
有一电视塔,在其东南方A处看塔顶时仰角为45°,在其西南方B处看塔顶时仰角为60°,若AB=120米,则电视塔的高度为( ).
A.60 米 米 | B.60米 | C.60 米或60米 米或60米 | D.30米 |
在△ABC中,a=3,b= ,c=2,那么∠B等于( )
,c=2,那么∠B等于( )
| A.30° | B.45° | C.60° | D.120° |
 的三边之比为3:5:7,求这个三角形的最大角为( )
的三边之比为3:5:7,求这个三角形的最大角为( )
A. | B. | C. | D. |
 中,角
中,角 所对的边分别是
所对的边分别是 ,若角
,若角 依次成等差数列,且
依次成等差数列,且 则
则 等于
等于
A. | B. | C. | D. |
在△ABC中,a=
 ,b=
,b= ,B=45°,则A等于( )
,B=45°,则A等于( )
| A.30° | B.60° | C.60°或120° | D.30°或150° |