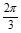题目内容
的三边之比为3：5：7，求这个三角形的最大角为（ ）
A． | B． | C． | D． |
C
解析试题分析：设出三边的长度，用余弦定理直接求解，此题中给的是三边长度的比例，可将其按比例设为3t，5t，7t，其中t＞0．
∵△ABC的三边之比为3：5：7，
∴设三边长依次为3t，5t，7t，其中t＞0,设最大角是C，由余弦定理知，
∴
=-
，所以C=120°
故应选C
考点：余弦定理
点评：知三边长的比值一般按比例用一个参数表示三个量，这样求边长时可以少建立方程，利于减少运算量．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在
中，
分别是角
所对的边,若
，则c="(" )
A． | B． | C． | D． |
在△ABC中，
，
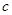=10，A=30°，则B=( )
| A．105° | B．60° | C．15° | D．105°或15° |
，则角A的大小为( ) 
B. 
C. 
D. 
在△ABC中，A＝60°，b＝1，其面积为
，则
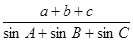等于( )
| A．3 | B． |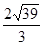
C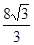． | D． |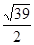
在
内，内角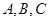
的对边分别是
，若
，
，则A=（ ）
A． | B． | C． | D． |
在
中，
分别为角
所对边，若
，则此三角形一定是( )
| A．等腰直角三角形 | B．直角三角形 | C．等腰三角形 | D．等腰或直角三角形 |
在△
中，
，
，
，在线段
上任取一点
，使△
为钝角三角形的概率为
A． | B． | C． | D． |
ac，则角B=
B.
C.
D.