题目内容
有一电视塔，在其东南方A处看塔顶时仰角为45°，在其西南方B处看塔顶时仰角为60°，若AB＝120米，则电视塔的高度为( )．
A．60 米 | B．60米 | C．60米或60米 | D．30米 |
A
解析试题分析：根据题意，设塔底的根基处为C，塔顶为D，则由于CD垂直于平面ABC，则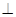DC
BC,D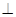CAC,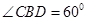
,
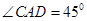在直角三角形BCD和ACD中，由三角函数的你故意可知DC=
,
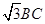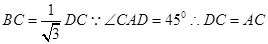,根据方位角可知
故可
,故选A.
考点：解三角形
点评：解决的关键是通过题意，作出三角形，利用平面图形来解决边和角的问题，进而得到高度，属于击锤他。
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
,则线段AM的长度是( )
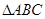中，若
，则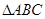的面积为 （ ）
A． | B． | C．1 | D． |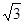
在△ABC中，
，
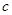=10，A=30°，则B=( )
| A．105° | B．60° | C．15° | D．105°或15° |
在△ABC中，若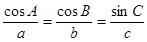
，则△ABC是（ ）
| A．有一内角为30°的直角三角形 | B．等腰直角三角形 |
| C．有一内角为30°的等腰三角形 | D．等边三角形 |
，则角A的大小为( ) 
B. 
C. 
D. 
在△ABC中，A＝60°，b＝1，其面积为
，则
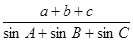等于( )
| A．3 | B． |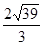
C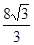． | D． |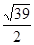
在
中，
分别为角
所对边，若
，则此三角形一定是( )
| A．等腰直角三角形 | B．直角三角形 | C．等腰三角形 | D．等腰或直角三角形 |
在△ABC中，
，则
等于( )
A． | B． | C． | D． |