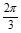题目内容
在△ABC中,a=
 ,b=
,b= ,B=45°,则A等于( )
,B=45°,则A等于( )
| A.30° | B.60° | C.60°或120° | D.30°或150° |
C.
解析试题分析:由正弦定理,得: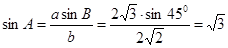 ,又因为A为三角形的内角,所以A=60°或120°。
,又因为A为三角形的内角,所以A=60°或120°。
考点:本题考查正弦定理。
点评:正弦定理通常用来解决:①已知两角和任一边,求另一角和其他两边;②已知两边和其中一边的对角,求另一边和其他两角。对于②这种类型的题,一定要注意判断解的个数,其实这种情况下用余弦定理更好些,可以免掉判断解的个数。

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
在△ 中,
中, ,
, ,
, ,在线段
,在线段 上任取一点
上任取一点 ,使△
,使△ 为钝角三角形的概率为
为钝角三角形的概率为
A. | B. | C. | D. |
在 中,
中, ,若以
,若以 为焦点的椭圆经过点
为焦点的椭圆经过点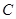 ,则该椭圆的离心率
,则该椭圆的离心率 ( )
( )
A. | B. | C. | D.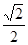 |
在△ABC中, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知 是
是 的一个内角,若
的一个内角,若 ,则
,则 是( )
是( )
| A.钝角三角形 | B.锐角三角形 |
| C.直角三角形 | D.任意三角形 |
下列已知△ABC的两边及其中一边对角的条件中,正确的是( )
A. 有两解 有两解 | B. 有一解 有一解 |
C. 无解 无解 | D. 有一解 有一解 |
在△ 中,若
中,若 ,则△
,则△ 是
是
| A.锐角三角形 | B.等腰三角形 | C.钝角三角形 | D.直角三角形 |
 ,则角A的大小为( )
,则角A的大小为( )  B.
B.  C.
C.  D.
D. 
 ac,则角B=
ac,则角B= B.
B. C.
C. D.
D.