Question

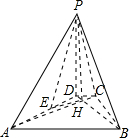如图，已知四棱锥P-ABCD的底面为等腰梯形，AB∥CD，AC⊥BD，垂足为H，PH是四棱锥的高，E为AD中点
（1）证明：PE⊥BC
（2）若∠APB=∠ADB=60°，求直线PA与平面PEH所成角的正弦值．

Answer 1

分析：以H为原点，HA，HB，HP分别为x，y，z轴，线段HA的长为单位长，建立空间直角坐标系．
（1）表示

PE

，

BC

，计算

.

PE

•

.

BC

=0，就证明PE⊥BC．
（2）∠APB=∠ADB=60°，求出C，P的坐标，再求平面PEH的法向量，
求向量

PA

，然后求

PA

与面PEH的法向量的数量积，可求直线PA与平面PEH所成角的正弦值．

解答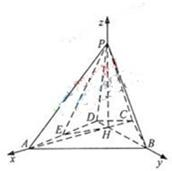：解：以H为原点，HA，HB，HP分别为x，y，z轴，线段HA的长为单位长，
建立空间直角坐标系如图，则A（1，0，0），B（0，1，0）
（Ⅰ）设C（m，0，0），P（0，0，n）（m＜0，n＞0）
则D(0，m，0)，E(

1

2

，

m

2

，0)．
可得

.

PE

=(

1

2

，

m

2

，-n)，

.

BC

=(m，-1，0)．
因为

.

PE

•

.

BC

=

m

2

-

m

2

+0=0
所以PE⊥BC．

（Ⅱ）由已知条件可得m=-

3

3

，n=1，故C（-

3

3

，0，0），D(0，-

3

3

，0)，E(

1

2

，-

3

6

，0)，P(0，0，1)
设

n

=（x，y，z）为平面PEH的法向量
则

n • HE =0 n • HP =0

即

1 2 x- 3 6 y=0 z=0

因此可以取

n

=(1，

3

，0)，
由

PA

=(1，0，-1)，
可得|cos＜

PA

，

n

＞|=

2

4

所以直线PA与平面PEH所成角的正弦值为

2

4

．

点评：本题主要考查空间几何体中的位置关系、线面所成的角等知识，考查空间想象能力以及利用向量法研究空间的位置关系以及线面角问题的能力．