题目内容
已知函数f(x)=ln ,若f(a)+f(b)=0,且0<a<b<1,则ab的取值范围是________.
,若f(a)+f(b)=0,且0<a<b<1,则ab的取值范围是________.
 ,若f(a)+f(b)=0,且0<a<b<1,则ab的取值范围是________.
,若f(a)+f(b)=0,且0<a<b<1,则ab的取值范围是________.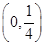
题意可知ln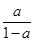 +ln
+ln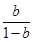 =0,
=0,
即ln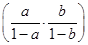 =0,从而
=0,从而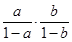 =1,
=1,
化简得a+b=1,
故ab=a(1-a)=-a2+a=-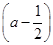 2+
2+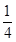 .
.
又0<a<b<1,故0<a<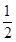 ,
,
故0<-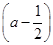 2+
2+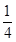 <
<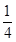 .
.
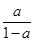 +ln
+ln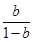 =0,
=0,即ln
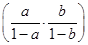 =0,从而
=0,从而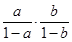 =1,
=1,化简得a+b=1,
故ab=a(1-a)=-a2+a=-
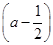 2+
2+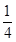 .
.又0<a<b<1,故0<a<
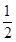 ,
,故0<-
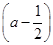 2+
2+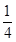 <
<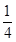 .
.
练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
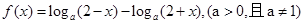
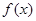 的奇偶性,并说明理由。
的奇偶性,并说明理由。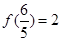 ,求使
,求使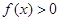 成立
成立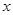 的集合。
的集合。 ,
, 的值域是 .
的值域是 . f(x)=x的根从小到大构成数列{an},则a2 012=________.
f(x)=x的根从小到大构成数列{an},则a2 012=________.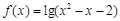 ,x∈R},B={x||x-i|<
,x∈R},B={x||x-i|<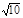 ,i为虚数单位,x>0},则A
,i为虚数单位,x>0},则A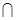 B=( )
B=( ) .
.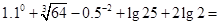 .
.