题目内容
对于函数f(x),若存在x0∈R, 使f(x0)=x0成立,则称x0为f(x)的“滞点”.已知函数f(x)=![]() ,
,
(1)试问f(x)有无“滞点”?若有求之,否则说明理由;
(2)已知数列{an}的各项均为负数,且满足4Sn·f(![]() )=1,求数列{an}的通项公式;
)=1,求数列{an}的通项公式;
(3)已知bn=an·2n,求{bn}的前n项和Tn.
解:(1)由f(x)=![]() ,令f(x)=x,得x2-2x=0,解得x=0,或x=2,
,令f(x)=x,得x2-2x=0,解得x=0,或x=2,
∴f(x)存在两个滞点0和2.
(2)由题意得4Sn·(![]() )2=2(
)2=2(![]() -1),
-1),
∴2Sn=an-an2.①
故2Sn+1=an+1-a n+12.②
由②-①得2an+1=an+1-an+12-an+an2,
∴(an+1+an)(an+1 -an+1)=0,
∴an<0,∴an+1-an=-1, 即{an}是等差数列,且d=-1.当n=1时,由2S1=a1-a12=2a1
得a1=-1,∴an=-n,
(3)∵Tn=-1·2-2·22-3·23-…-n·2n,③
∴2Tn=-1·22-2·23-3·24-…-(n-1)·2n-n·2n+1,④
由④-③得Tn=2+22+23+…+2n-n·2n+1=![]() -n·2n+1=2n+1-2-n·2n+1.
-n·2n+1=2n+1-2-n·2n+1.

练习册系列答案
相关题目
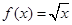 的等域区间是 .
的等域区间是 .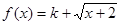 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.