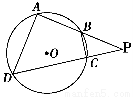
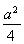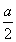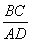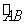题目内容
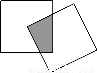
如图所示,已知AB是⊙O的直径,C为圆上任意一点,过C的切线分别与过A、B两点的切线交于P、Q.
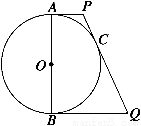
求证:AB2=4AP·BQ.
见解析
【解析】
证明 法一 连接OP、OQ,如图所示.
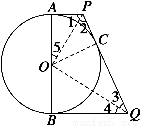
∵AP、PQ、BQ为⊙O的切线,
∴∠1=∠2,∠3=∠4.
又AP、BQ为⊙O的切线,
AB为直径,∴AB⊥AP,AB⊥BQ.
∴AP∥BQ.
∴∠A=∠B=90°,
∠1+∠2+∠3+∠4=180°.
∴∠1+∠4=∠2+∠3=90°.
∵∠1+∠5=90°,∴∠4=∠5.
∴△AOP∽△BQO.
∴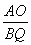 =
=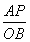 .
.
∵AB=2AO=2OB,∴AB2=4AP·BQ.
法二 连接OC.
同上可证得∠2+∠3=90°.
∵PQ切⊙O于C,∴OC⊥PQ.
在Rt△PQO中,由射影定理可得OC2=PC·CQ,
利用切线长定理,有PC=AP,BQ=QC.
OC2=AP·BQ,∵AB=2OC,∴AB2=4AP·BQ.
法三 如图所示,过P作BQ的垂线PD,垂足为D.
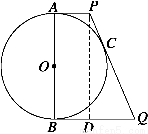
∵AP、BQ、PQ切⊙O于A、B、C,
∴∠A=∠B=90°,
AP=PC,CQ=BQ.
∴四边形ABDP为矩形,
PQ=AP+BQ.∵AP=BD,AB=PD.
在Rt△PQD中,利用勾股定理得:PQ2=PD2+QD2,
∴(AP+BQ)2=AB2+(BQ-AP)2.
∴4AP·BQ=AB2.

练习册系列答案
相关题目