题目内容
已知集合A={y|y=-2x,x∈[2,3]},B={x|x2+3x-a2-3a>0}.若A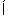 B,求实数a的取值范围.
B,求实数a的取值范围.
(-4,1)
【解析】由题意有A=[-8,-4],B={x|(x-a)(x+a+3)>0}.
① 当a=-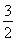 时,B=
时,B=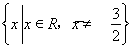 ,所以A
,所以A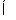 B恒成立;
B恒成立;
② 当a<-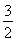 时,B={x|x<a或x>-a-3}.因为A
时,B={x|x<a或x>-a-3}.因为A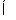 B,所以a>-4或-a-3<-8,解得a>-4或a>5(舍去),所以-4<a<-
B,所以a>-4或-a-3<-8,解得a>-4或a>5(舍去),所以-4<a<-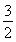 ;
;
③ 当a>-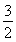 时,B={x|x<-a-3或x>a}.因为A?B,所以-a-3>-4或a<-8(舍去),解得-
时,B={x|x<-a-3或x>a}.因为A?B,所以-a-3>-4或a<-8(舍去),解得-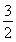 <a<1.
<a<1.
综上,当A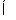 B时,实数a的取值范围是(-4,1).
B时,实数a的取值范围是(-4,1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目