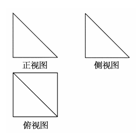
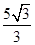题目内容
如图,在直三棱柱ABC A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F分别是A1C1,BC的中点.

(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P B1C1F的体积.

(1)证明:平面AEB⊥平面BB1C1C;
(2)证明:C1F∥平面ABE;
(3)设P是BE的中点,求三棱锥P B1C1F的体积.
(1) (2)见解析 (3)

(1)证明 在△ABC中,∵AC=2BC=4,∠ACB=60°,由余弦定理得:
∴AB=2
 ,∴AB2+BC2=AC2,
,∴AB2+BC2=AC2,∴AB⊥BC,
由已知AB⊥BB1,又BB1∩BC=B,∴AB⊥面BB1C1C,
又∵AB?面ABE,∴平面ABE⊥平面BB1C1C.
(2)证明 取AC的中点M,连接C1M,FM
在△ABC,FM∥AB,而FM?平面ABE,AB?平面ABE,
∴直线FM∥平面ABE
在矩形ACC1A1中,E,M都是中点,∴C1E綉AM,四边形AMC1B是平面四边形,∴C1M∥AE
而C1M?平面ABE,AE?平面ABE,∴直线C1M∥ABE
又∵C1M∩FM=M,∴平面ABE∥平面FMC1,而CF1?平面FMC1,
故C1F∥平面AEB.
(3)解 取B1C1的中点H,连接EH,则EH∥A1B1,所以EH∥AB且EH=
 AB=
AB= ,
,由(1)得AB⊥面BB1C1C,∴EH⊥面BB1C1C,
∵P是BE的中点,
∴VPB1C1F=
 VEB1C1F=
VEB1C1F= ×
× S△B1C1F·EH=
S△B1C1F·EH=

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 中,
中, 底面
底面 ,底面
,底面 ,
, 是
是 的中点。
的中点。
 ;
;  ;
; ,求二面角
,求二面角 的余弦值.
的余弦值.