题目内容
已知一个四棱锥P－ABCD的三视图(正视图与侧视图为直角三角形，俯视图是带有一条对角线的正方形)如图，E是侧棱PC的中点．
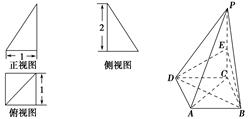
(1)求四棱锥P－ABCD的体积；
(2)求证：平面APC⊥平面BDE.
(1)求四棱锥P－ABCD的体积；
(2)求证：平面APC⊥平面BDE.
（1）
（2）见解析
（2）见解析(1)由三视图可知，AB＝BC＝1，PC⊥平面ABCD，且PC＝2，
又底面ABCD是正方形，故S正方形ABCD＝1，所以VP－ABCD＝
×1×2＝.
(2)因为底面ABCD是正方形，所以对角线AC⊥BD，
又PC⊥平面ABCD，而BD?平面ABCD，故BD⊥PC，
又PC∩AC＝C，所以，BD⊥平面APC.
又BD?平面BDE，故平面APC⊥平面BDE.
又底面ABCD是正方形，故S正方形ABCD＝1，所以VP－ABCD＝
×1×2＝.(2)因为底面ABCD是正方形，所以对角线AC⊥BD，
又PC⊥平面ABCD，而BD?平面ABCD，故BD⊥PC，
又PC∩AC＝C，所以，BD⊥平面APC.
又BD?平面BDE，故平面APC⊥平面BDE.
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
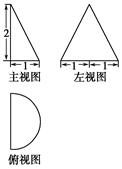
）如图所示，则此几何体的体积是( )
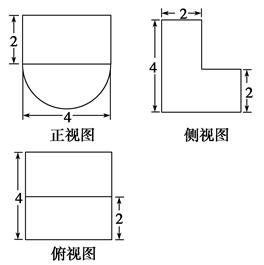
的小正方形，在其上用粗线画出了一四棱锥的三视图，则该四棱锥的体积为（ ）
