题目内容
【题目】设![]() 、
、![]() 分别是椭圆C:
分别是椭圆C:![]() 的左、右焦点,
的左、右焦点,![]() ,直线1过
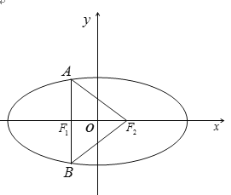
,直线1过![]() 且垂直于x轴,交椭圆C于A、B两点,连接A、B、
且垂直于x轴,交椭圆C于A、B两点,连接A、B、![]() ,所组成的三角形为等边三角形。
,所组成的三角形为等边三角形。
(1)求椭圆C的方程;
(2)过右焦点![]() 的直线m与椭圆C相交于M、N两点,试问:椭圆C上是否存在点P,使
的直线m与椭圆C相交于M、N两点,试问:椭圆C上是否存在点P,使![]() 成立?若存在,求出点P的坐标;若不存在,说明理由.
成立?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)椭圆![]() ;(2)
;(2)![]()
【解析】
(1)由题意布列关于a,b的方程组,解之,即可得到椭圆C的方程;
(2)设![]() 、
、![]() ,设y=k(x﹣1)(k≠0),代入椭圆方程得
,设y=k(x﹣1)(k≠0),代入椭圆方程得![]() ,由此运用韦达定理和向量的坐标运算,代入椭圆方程,解得k,求出点P的坐标.
,由此运用韦达定理和向量的坐标运算,代入椭圆方程,解得k,求出点P的坐标.
(1)
由![]() 可得
可得![]() ,
,
等边三角形![]() 中:
中:![]() ,
,![]() ,
,
则![]()
![]() ,得
,得![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
则椭圆![]() ;
;
(2)设![]() 、
、![]() ,
,
则由题意知的![]() 斜率为一定不为
斜率为一定不为![]() ,故不妨设
,故不妨设![]() ,
,
代入椭圆![]() 的方程中,
的方程中,
整理得![]() ,
,
显然![]() .
.
由韦达定理有:![]() ,
,![]() ①
①
且![]() ②
②
假设存在点![]() ,使
,使![]() 成立,则其充要条件为:
成立,则其充要条件为:
点![]() ,
,
点![]() 在椭圆上,即
在椭圆上,即![]() .
.
整理得![]()
又![]() 在椭圆上,即
在椭圆上,即![]() ,
,![]() ,
,
故由①②代入:![]() ,解得
,解得![]() ,
,
则![]() 。
。

练习册系列答案
相关题目
【题目】A市某机构为了调查该市市民对我国申办2034年足球世界杯的态度,随机选取了140位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 | 60 | ||
女性市民 | 50 | ||
合计 | 70 | 140 |
(1)根据已知数据,把表格数据填写完整;
(2)若在被调查的支持申办足球世界杯的男性市民中有5位退休老人,其中2位是教师,求从这5人中随机抽取3人至多有1人是教师的概率.


