题目内容
命题“对 ”的否定是( )
”的否定是( )
| A.不存在x∈R,x3-x2+1≤0 | B. |
C. | D. |
C
解析试题分析:因为全称命题的否定是特称命题。所以“对 ”的否定是:
”的否定是: ,故选C
,故选C
考点:本题主要考查全称命题与特称命题的之间的关系的应用。
点评:基础题,全称命题的否定是特称命题。

练习册系列答案
相关题目
已知直线a和两个平面 ,给出下列两个命题:
,给出下列两个命题:
命题p:若a∥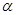 ,a⊥
,a⊥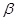 ,则
,则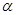 ⊥
⊥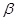 ;
;
命题q:若a∥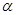 , a∥
, a∥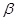 ,则
,则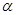 ∥
∥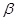 。
。
那么下列判断正确的是( )
| A.p为假 | B. 为假 为假 | C.p∧q为真 | D.p∨q为真 |
设命题甲: 的解集是实数集R;命题乙:
的解集是实数集R;命题乙: ,则命题甲是命题乙成的( )
,则命题甲是命题乙成的( )
| A.充要条件 |
| B.充分非必要条件 |
| C.必要非充分条件 |
| D.既非充分又非必要条件 |
设命题甲: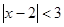 ;命题乙:
;命题乙: ,那么甲是乙的( )
,那么甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在原命题及其逆命题、否命题、逆否命题这四个命题中,真命题的个数可以是
| A.1个或2个或3个或4个 |
| B.0个或2个或4个 |
| C.1个或3个 |
| D.0个或4个 |
设 是两个不共线的非零向量,则“向量
是两个不共线的非零向量,则“向量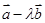 与
与 共线”是“
共线”是“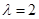 ”
”
的( )
| A.充分非必要条件 | B.必要非充分条件 | C.充要条件 | D.非充分非必要条件 |
在 中,“
中,“ ”是“
”是“ ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 :x
:x -x-20>0,
-x-20>0, :
: <0,则
<0,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |