题目内容
【题目】如图，在直三棱柱
中，∠BAC=90°，AB=AC=AA1=2，E是BC中点．
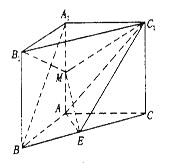
(Ⅰ)求证：A1B//平面AEC1；
(Ⅱ)在棱AA1上存在一点M，满足
，求平面MEC1与平面ABB1A1所成锐二面角的余弦值。
【答案】（Ⅰ）见解析；(Ⅱ) 
.
【解析】试题分析： 
连接
交
于点
，连接
，推导出
，由此能证明
平面
； 
以
为原点， 
为
轴， 
为
轴， 
为
轴，建立空间直角坐标系，利用向量法能求出平面
与平面
所成锐二面角的余弦值
解析：（Ⅰ）证明：连接
交
于O，连接EO.
因为
为正方形，
所以O为
的中点，
而E为CB的中点，
所以EO为△
的中位线，
则
，
又
平面
, 
平面
, 
平面
.
(Ⅱ)以点A为原点建立如图所示的空间直角坐标系，
则
,
设
，
所以
,
，
,
设平面MEC1的法向量为
，则
，
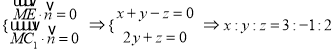取
，
∵AC⊥平面ABB1A1,取平面ABB1A1的法向量
,
，
平面MEC1与平面ABB1A1所成锐二面角的余弦值
.
练习册系列答案
相关题目
【题目】小萌大学毕业后，家里给了她10万元，她想办一个“萌萌”加工厂，根据市场调研，她得出了一组毛利润
（单位：万元）与投入成本
（单位：万元）的数据如下：
投入成本 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 |
毛利润 | 1.06 | 1.25 | 2 | 3.25 | 5 | 7.25 | 9.98 |
为了预测不同投入成本情况下的利润，她想在两个模型
，
中选一个进行预测.
（1）根据投入成本2万元和4万元的两组数据分别求出两个模型的函数解析式，请你根据给定数据选出一个较好的函数模型进行预测（不必说明理由），并预测她投入8万元时的毛利润；
（2）若小萌准备最少投入2万元开办加工厂，请预测加工厂毛利润率
的最大值，并说明理由.（
）
