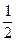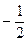题目内容
设有函数f(x)=asin(kx+
)和φ(x)=btan(kx-
)，k＞0，若它们的最小正周期的和为
，且f(
)=ϕ(
)，f(
)=-
ϕ(
)+1，求f（x）和ϕ（x）的解析式．
| π |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 3 |
| π |
| 4 |
f（x）的最小正周期为
，ϕ（x）的最小正周期为
，
依题意知：
+
=
，解得k=2，
∴f（x）=asin（2x+
），φ（x）=btan（2x-
），
∵
，
∴
，
即
，
解得：
，
∴f（x）=sin（2x+
），φ（x）=
tan（2x-
）．
| 2π |
| k |
| π |
| k |
依题意知：
| 2π |
| k |
| π |
| k |
| 3π |
| 2 |
∴f（x）=asin（2x+
| π |
| 3 |
| π |
| 3 |
∵
|
∴
|
即
|
解得：
|
∴f（x）=sin（2x+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
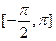上的函数y＝f（x）的图象关于直线
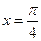对称，当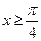
时，函数f（x）＝sinx．
，
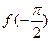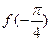的值；
的值为（ ）
（ ）
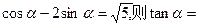