题目内容
8.在平面直角坐标系xOy中,△OBC的边BC所在的直线方程是l:x-y-3=0(1)如果一束光线从原点O射出,经直线l反射后,经过点(3,3),求反射后光线所在直线的方程:
(2)如果在△OBC中,∠BOC为直角,求△OBC面积的最小值.
分析 (1)由题意可知反射光线经过原点关于了的对称点和(3,3),由对称关系求出点的坐标可得直线方程;
(2)由题意设B(x1,x1-3),C(x2,x2-3),由直角可得x1+x2=$\frac{1}{3}$(2x1x2+9),由距离公式可得BC|的表达式,由二次函数可得.
解答 解:(1)设原点O(0,0)关于l的对称点为(m,n),
则$\left\{\begin{array}{l}{\frac{n-0}{m-0}•1=-1}\\{\frac{m}{2}-\frac{n}{2}-3=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=3}\\{n=-3}\end{array}\right.$,
由题意可知反射光线经过点(3,-3)和(3,3),
∴反射光线所在直线的方程为x=3;
(2)由题意设B(x1,x1-3),C(x2,x2-3),
∵∠BOC为直角,∴x1x2+(x1-3)(x2-3)=0,
化简可得x1+x2=$\frac{1}{3}$(2x1x2+9),
∴}BC|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({x}_{1}-3-{x}_{2}+3)^{2}}$
=$\sqrt{2}$•$\sqrt{({x}_{1}-{x}_{2})^{2}}$=$\sqrt{2}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$,
=$\sqrt{2}$•$\sqrt{\frac{1}{3}}$•$\sqrt{4({x}_{1}{x}_{2})^{2}+81}$
由二次函数可知当x1x2=0时,上式取最小值3$\sqrt{6}$.
点评 本题考查直线的对称性,涉及直线垂直关系和二次函数的最值,属中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2005 | B. | 2007 | C. | 2009 | D. | 2011 |
| A. | 0 | B. | 1 | C. | 1或4 | D. | 无法确定 |
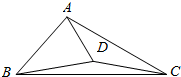 已知∠BAC>90°,∠ACB=30°,AB=DB=DC,求∠CAD的度数.
已知∠BAC>90°,∠ACB=30°,AB=DB=DC,求∠CAD的度数.