题目内容
18.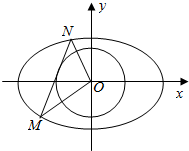 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点到两焦点的距离和为$\frac{2}{3}$,短轴长为$\frac{1}{2}$,直线l与椭圆C交于M,N两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点到两焦点的距离和为$\frac{2}{3}$,短轴长为$\frac{1}{2}$,直线l与椭圆C交于M,N两点.(Ⅰ)求椭圆C方程;
(Ⅱ)若直线MN与圆O:x2+y2=$\frac{1}{25}$相切,证明:∠MON为定值;
(Ⅲ)在(Ⅱ)的条件下,求|OM||ON|的取值范围.
分析 (1)利用椭圆的定义进行求解;
(2)利用圆心到直线的距离,求出直线的斜率与截距的关系,再利用平面向量的数量积求证角为定值;
(3)利用三角换元进行求解.
解答  解:(Ⅰ)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点到两焦点的距离和为$\frac{2}{3}$,得2a=$\frac{2}{3}$,即a=$\frac{1}{3}$;
解:(Ⅰ)由椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的点到两焦点的距离和为$\frac{2}{3}$,得2a=$\frac{2}{3}$,即a=$\frac{1}{3}$;
由短轴长为$\frac{1}{2}$,得2b=$\frac{1}{2}$,即b=$\frac{1}{4}$
所以椭圆C方程:9x2+16y2=1
(Ⅱ)当直线MN⊥x轴时,因为直线MN与圆O:x2+y2=$\frac{1}{25}$相切,
所以直线MN方程:x=$\frac{1}{5}$或x=-$\frac{1}{5}$,
当直线方程为x=$\frac{1}{5}$,得两点分别为($\frac{1}{5}$,$\frac{1}{5}$)和($\frac{1}{5}$,-$\frac{1}{5}$),故$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,
所以∠MON=$\frac{π}{2}$;同理可证当x=-$\frac{1}{5}$,∠MON=$\frac{π}{2}$;
当直线MN与x轴不垂直时,设直线MN:y=kx+b,直线MN与圆O:x2+y2=$\frac{1}{25}$的交点M(x1,y1),N(x2,y2),
由直线MN与圆O相切得d=$\frac{|b|}{\sqrt{{k}^{2}+1}}$=$\frac{1}{5}$,即25b2=k2+1,①
联立y=kx+b与椭圆方程,得(9+16k2)x2+32kbx+16b2-1=0,
∴△>0,x1+x2=-$\frac{32kb}{9+16{k}^{2}}$,x1x2=$\frac{16{b}^{2}-1}{9+16{k}^{2}}$,
$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=x1x2+(kx1+b)(kx2+b)=$\frac{25{b}^{2}-{k}^{2}-1}{9+16{k}^{2}}$,②
由①②,得$\overrightarrow{OM}$•$\overrightarrow{ON}$=0,即∠MON=$\frac{π}{2}$,
综上,∠MON=$\frac{π}{2}$为定值.
(Ⅲ)不妨设∠XOM=θ,则∠XON=θ±$\frac{π}{2}$,
由三角函数定义可知:M(|OM|cosθ,|OM|sinθ),N(±|ON|sinθ,±|ON|cosθ)
因为点M、N都在9x2+16y2=1上,
所以$\frac{1}{|OM{|}^{2}}$=9cos2θ+16sin2θ,$\frac{1}{|ON{|}^{2}}$=9sin2θ+16cos2θ
$\frac{1}{|OM{|}^{2}}$•$\frac{1}{|ON{|}^{2}}$=(9cos2θ+16sin2θ)(9sin2θ+16cos2θ)
=9×16+(9-16)2sin2θcos2θ
=9×16+(9-16)2$\frac{1}{4}$sin22θ,
又sin22θ∈[0,1],故$\frac{1}{|OM{|}^{2}}$•$\frac{1}{|ON{|}^{2}}$∈[9×16,$\frac{625}{4}$],
∴|OM||ON|的取值范围是[$\frac{2}{25}$,$\frac{1}{12}$].
点评 本题考查椭圆方程的求法,考查角为定值的证明,考查线段的取值范围的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

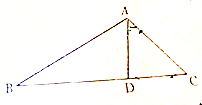 在△ABC中,AC=7,AD为∠BAC的角平分线交BC于D,且AD的长为整数,DC=4$\sqrt{2}$,cos∠DAC=$\frac{3}{5}$.
在△ABC中,AC=7,AD为∠BAC的角平分线交BC于D,且AD的长为整数,DC=4$\sqrt{2}$,cos∠DAC=$\frac{3}{5}$.