题目内容
已知函数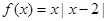
(1)写出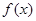 的单调区间
的单调区间
(2)解不等式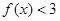
(3)设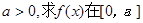 上的最大值
上的最大值
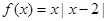
(1)写出
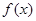 的单调区间
的单调区间(2)解不等式
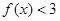
(3)设
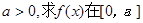 上的最大值
上的最大值∴f(x)的单调递增区间是(-∞,1]和[2,+∞);单调递减区间是[1,2]
⑵∵ 或
或
∴不等式f(x)<3的解集为{x|x<3}
⑶①当

②当1≤a≤2时,f(x)在[0 1]上是增函数,在[1,a]上是减函数,
此时f(x)在[0 a]上的最大值是f(1)=1
③当a>2时,令f(a)-f(1)=a(a-2)-1=a2-2a-1>0, 解得
ⅰ当2<a≤ 时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1
时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1
ⅱ当a> 时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)
时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)
综上,当0<a<1时,f(x)在[0,a]上的最大值是a(2-a);
⑵∵
 或
或
∴不等式f(x)<3的解集为{x|x<3}
⑶①当


②当1≤a≤2时,f(x)在[0 1]上是增函数,在[1,a]上是减函数,
此时f(x)在[0 a]上的最大值是f(1)=1
③当a>2时,令f(a)-f(1)=a(a-2)-1=a2-2a-1>0, 解得

ⅰ当2<a≤
 时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1
时,此时f(a)≤f(1),f(x)在[0,a]上的最大值是f(1)=1ⅱ当a>
 时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)
时,此时f(a)>f(1),f(x)在[0,a]上的最大值是f(a)=a(a-2)综上,当0<a<1时,f(x)在[0,a]上的最大值是a(2-a);
略

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 与
与 表示同一函数的是( )
表示同一函数的是( )
 ,
,
 ,
,
 ,
,

 .
. 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,求
,求 的值;
的值; 上不单调,求
上不单调,求 的取值范围.
的取值范围. ,上、下两边各空2
,上、下两边各空2 ,左、右两边各空1
,左、右两边各空1
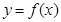 在
在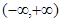 内有定义.对于给定的正数
内有定义.对于给定的正数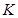 ,定义函数
,定义函数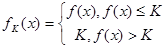 , 取函数
, 取函数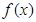 =
=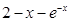 .若对任意的
.若对任意的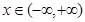 ,恒有
,恒有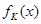 =
= 吨,应交水费
吨,应交水费 元。
元。 ,共交水费26.4元,分别求出甲、乙两用户该月的用水量和水费。
,共交水费26.4元,分别求出甲、乙两用户该月的用水量和水费。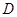 内的任意一个自变量
内的任意一个自变量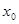 ,都有函数值
,都有函数值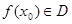 ,则称函数
,则称函数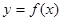 在
在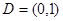 ,则函数①
,则函数①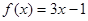 ;②
;②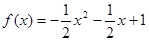 ;③
;③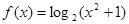 ;④
;④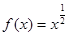 ,其中在
,其中在 满足
满足 =
= ,且在
,且在 时,
时, ,则关于
,则关于 的方程
的方程 ,在
,在 上解的个数是 .
上解的个数是 . ,关于
,关于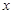 的方程
的方程 的四个实根构成以
的四个实根构成以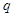 为公比的等比数列,若
为公比的等比数列,若 ,则
,则 的取值范围是 .
的取值范围是 .