题目内容
已知f(x)是定义在(0,+∞)上的增函数,f(x)>0且f(3)=1,指出函数F(x)=f(x)+
思路分析:这道题要求先写出单调区间,但单调区间无法从函数解析式上观察出来.也无法画出函数的图象,再从图象上看出来.故只能根据函数的单调性的定义,直接进行演绎推理.由已知条件f(3)=1,猜测:3可能是单调区间的一个端点.?
解:设0<x1<x2,则?
F(x2)-F(x1)=f(x2)+![]() -[f(x1)+
-[f(x1)+![]() ]
]
=[f(x2)-f(x1)]·[1-![]() ].?
].?
当0<x1<x2≤3时,0<f(x1)<f(x2)≤f(3) =1,?
∴f(x2)-f(x1)>0,1-![]() <0.?
<0.?
∴F(x2)-F(x1)<0,F(x2)<F(x1).?
∴F(x)在(0,3]上是减函数.?
当3≤x1<x2时,1=f(3)≤f(x1)<f(x2),?
∴f(x2)-f(x1)>0,1-![]() >0.?
>0.?
∴F(x2)-F(x1)>0,F(x2)>F(x1).?
∴F(x)在[3,+∞)上是增函数.

练习册系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 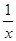 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
