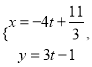题目内容
【题目】设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,方程
时,方程![]() 在区间
在区间![]() 内有唯一实数解,求实数
内有唯一实数解,求实数![]() 的取值范围
的取值范围
【答案】(Ⅰ)单调增区间为![]() ,减区间为
,减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() .或
.或![]()
【解析】
试题分析:(Ⅰ)先确定函数定义域![]() ,再求导函数
,再求导函数![]() ,进而求定义区间上导函数的零点
,进而求定义区间上导函数的零点![]() ,最后列表分析导函数符号:当
,最后列表分析导函数符号:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,确定单调区间:增区间为
,确定单调区间:增区间为![]() ,减区间为
,减区间为![]() ;(Ⅱ)化简方程得
;(Ⅱ)化简方程得![]() ,变量分离得
,变量分离得![]() ,利用导数研究函数
,利用导数研究函数![]() 单调性变化规律:在区间
单调性变化规律:在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数.最后结合图像确定有唯一解的条件:
上是减函数.最后结合图像确定有唯一解的条件:![]() .或
.或![]()
试题解析:(1)依题意,知![]() 的定义域为
的定义域为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() …………………………………2分
…………………………………2分
令![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 的单调增区间为
的单调增区间为![]() ,减区间为
,减区间为![]() ; …………………5分
; …………………5分
(2)当![]() 时,
时,![]() ,
,
由![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() ,
,
要使方程![]() 在区间
在区间![]() 上有唯一实数解,
上有唯一实数解,
只需![]() 有唯一实数解, ………………………7分
有唯一实数解, ………………………7分
令![]() ,
,
∴![]() ,
,
由![]() 得
得![]() ;
; ![]() ,得
,得![]() ,
,
∴![]() 在区间
在区间![]() 上是增函数,在区间
上是增函数,在区间![]() 上是减函数.
上是减函数.
![]() ,故
,故 ![]() .或
.或![]() ……………13分
……………13分

练习册系列答案
相关题目
【题目】经统计,某医院一个结算窗口每天排队结算的人数及相应的概率如下:
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
(1)求每天超过20人排队结算的概率;
(2)求2天中,恰有1天出现超过20人排队结算的概率.
【题目】下表提供了某厂生产某产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 2 | 4 | 6 | 8 | 10 |
| 4 | 5 | 7 | 9 | 10 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)中求出的线性回归方程,预测生产20吨该产品的生产能耗是多少吨标准煤?
附:回归直线的斜率和截距的最小二乘估计分别为: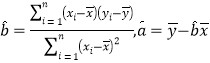 .
.