题目内容
设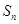 是数列
是数列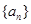 的前
的前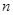 项和,且
项和,且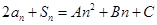 .
.
(1)当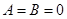 ,
,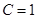 时,求
时,求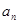 ;
;
(2)若数列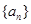 为等差数列,且
为等差数列,且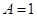 ,
,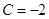 .
.
①求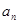 ;
;
②设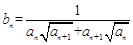 ,且数列
,且数列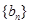 的前
的前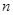 项和为
项和为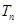 ,求
,求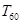 的值.
的值.
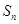 是数列
是数列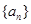 的前
的前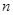 项和,且
项和,且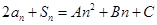 .
.(1)当
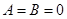 ,
,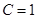 时,求
时,求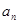 ;
; (2)若数列
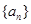 为等差数列,且
为等差数列,且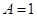 ,
,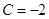 .
.①求
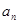 ;
;②设
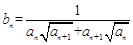 ,且数列
,且数列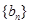 的前
的前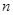 项和为
项和为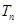 ,求
,求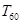 的值.
的值.(1) ;(2)①
;(2)①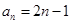 ;②
;②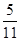
 ;(2)①
;(2)①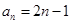 ;②
;②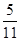
试题分析:(1)令n=1,先求出
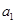 ,再利用
,再利用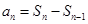 导出
导出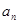 的递推公式,由递推公式知数列{
的递推公式,由递推公式知数列{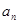 }是等比数列,利用等比数列通项公式通项公式写出
}是等比数列,利用等比数列通项公式通项公式写出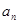 ;(2)由等差数列通项公式和前n项和公式代入已知条件
;(2)由等差数列通项公式和前n项和公式代入已知条件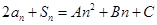 ,通过比较系数求得
,通过比较系数求得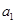 与
与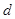 ,从而写出
,从而写出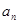 ;将
;将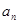 代入
代入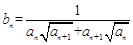 求出数列
求出数列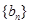 的通项公式,通过提前公因式、分母有理化将
的通项公式,通过提前公因式、分母有理化将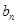 拆成两项的差,利用拆项消去法求出
拆成两项的差,利用拆项消去法求出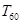 .
.试题解析:(1)由题意得,
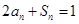 ,
,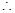
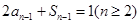 ,
,两式相减,得
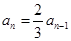 , 3分
, 3分又当
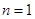 时,有
时,有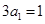 ,即
,即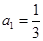 ,
,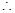 数列
数列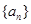 为等比数列,
为等比数列,
 . 5分
. 5分(2)①
 数列
数列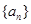 为等差数列,由通项公式与求和公式,
为等差数列,由通项公式与求和公式,得
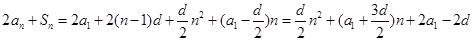 ,
,
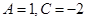 ,
, 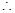
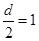 ,
,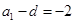 ,
,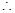
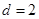 ,
,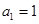 ,
,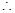
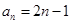 . 10分
. 10分②

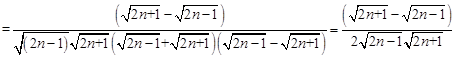
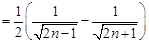 13分
13分则
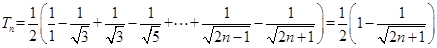 ,
,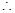
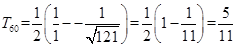 16分
16分考点:数列第n项与前n项和的关系;等比数列定义与通项公式;等差数列通项公式与前n项和公式;拆项消去法;转化与化归思想

练习册系列答案
相关题目
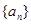 的前
的前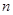 项和
项和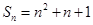 ,
,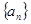 中,
中, ,求数列
,求数列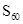
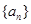 满足
满足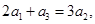 且
且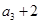 是
是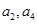 的等差中项
的等差中项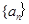 的通项公式;(2)若
的通项公式;(2)若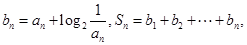 求使
求使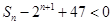 成立的正整数
成立的正整数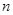 的最小值.
的最小值. 也是等比数列. 若数列
也是等比数列. 若数列 是等差数列,可类比得到关于等差数列的一个性质为( ).
是等差数列,可类比得到关于等差数列的一个性质为( ). 是等差数列
是等差数列 是等差数列
是等差数列 是等差数列
是等差数列 是等差数列
是等差数列 时,数列{an}为递减数列;②当
时,数列{an}为递减数列;②当 为正整数时,数列{an}必有两项相等的最大项
为正整数时,数列{an}必有两项相等的最大项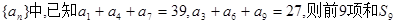 的值为( )
的值为( ) 前项和为
前项和为 ,且点
,且点 在
在 图像上,求
图像上,求