题目内容
9. 如图,已知MA为⊙O的切线,A为切点,△ABC是⊙O的内接三角形,MB交AC于D,交⊙O于E,若MA=MD,∠ABC=60°,ME=1,MB=9,则DC=4.
如图,已知MA为⊙O的切线,A为切点,△ABC是⊙O的内接三角形,MB交AC于D,交⊙O于E,若MA=MD,∠ABC=60°,ME=1,MB=9,则DC=4.
分析 利用切割线定理结合题中所给数据,得MA=3,由弦切角定理结合有一个角为60°的等腰三角形是正三角形,得到AD=MD=MA=3,最后由相交弦定理可得BD•DE=AD•CD,从而求出CD的长.
解答 解:∵MA是圆O的切线,
∴MA2=ME•MB=9,可得MA=3,
∵∠MAC是弦切角,夹弧AEC,
∴∠MAC=∠ABC=60°,
∵△MAD中,MA=MD,
∴△MAD是正三角形,可得AD=MD=MA=3,
∴BD=MB-MD=6,ME=MD-ED=2,
∵圆O中,弦AC、BE相交于D,
∴BD•DE=AD•CD,可得6×2=3CD,
∴CD=4,
故答案为:4.
点评 本题在圆中给出切线,并且以切线长为一边作正三角形的情况下,求线段的长度.着重考查了切线的性质、正三角形的判定和相交弦定理等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.关于x的方程(x2-1)2-3|x2-1|+2=0的不相同实根的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 8 |
20.一个几何体的三视图如图所示,则这个几何体的体积为( )
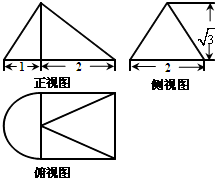

| A. | $\frac{{4\sqrt{3}}}{3}+\frac{{\sqrt{3}π}}{6}$ | B. | $\frac{{8\sqrt{3}}}{3}+\frac{{\sqrt{3}π}}{3}$ | C. | $\frac{{4\sqrt{3}}}{3}+\frac{{4\sqrt{3}π}}{3}$ | D. | $4\sqrt{3}+\sqrt{3}π$ |
14.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x<2}\\{x+y-1≥0}\end{array}\right.$,则z=2x-2y-3的取值范围是( )
| A. | [-$\frac{1}{3}$,3] | B. | [-2,3] | C. | [-$\frac{1}{3}$,3) | D. | $[-\frac{11}{3},3)$ |
18.不可能以直线$y=\frac{1}{2}x+b$作为切线的曲线是( )
| A. | y=sinx | B. | $y=\frac{1}{x}$ | C. | y=lnx | D. | y=ex |
 如图,四棱锥层-ABCD中,平面EAD⊥ABCD,CD∥AB,BC⊥CD,EA⊥ED.且AB=4,BC=CD=EA=ED=2
如图,四棱锥层-ABCD中,平面EAD⊥ABCD,CD∥AB,BC⊥CD,EA⊥ED.且AB=4,BC=CD=EA=ED=2