题目内容
14.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1≥0}\\{x<2}\\{x+y-1≥0}\end{array}\right.$,则z=2x-2y-3的取值范围是( )| A. | [-$\frac{1}{3}$,3] | B. | [-2,3] | C. | [-$\frac{1}{3}$,3) | D. | $[-\frac{11}{3},3)$ |
分析 根据画出不等式组表示的平面区域,利用数形结合结合目标函数的意义,利用平移即可得到结论.
解答 解:不等式对应的平面区域如图:(阴影部分). 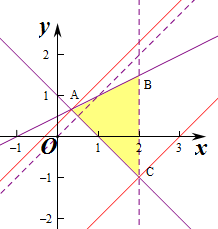
由z=2x-2y-3得y=x-$\frac{3+z}{2}$,平移直线y=x-$\frac{3+z}{2}$,
由平移可知当直线y=x-$\frac{3+z}{2}$,经过点C时,
直线y=x-$\frac{3+z}{2}$的截距最小,此时z取得最大值,
由$\left\{\begin{array}{l}{x=2}\\{x+y-1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$,即C(2,-1),
此时z=2x-2y-3=4+2-3=3,
可知当直线y=x-$\frac{3+z}{2}$,经过点A时,
直线y=y=x-$\frac{3+z}{2}$的截距最大,此时z取得最小值,
由$\left\{\begin{array}{l}{x-2y+1=0}\\{x+y-1=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{1}{3}}\\{y=\frac{2}{3}}\end{array}\right.$,即A($\frac{1}{3}$,$\frac{2}{3}$)
代入z=2x-2y-3得z=2×$\frac{1}{3}$-2×$\frac{2}{3}$-3=-$\frac{11}{3}$,
故z∈[-$\frac{11}{3}$,3)
故选:D.
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
相关题目
2.由y=$\frac{1}{x}$-1,y=0,x=2所对应的曲线围成的封闭图形的面积为( )
| A. | ln2-$\frac{1}{2}$ | B. | $\frac{1}{2}$-ln2 | C. | 1-ln2 | D. | ln2-1 |
6.函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期是π,若其图象向右平移$\frac{π}{3}$个单位后得到的函数为奇函数,则函数f(x)的图象( )
| A. | 关于点$(\frac{π}{6},0)$对称 | B. | 关于x=$\frac{π}{6}$对称 | C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于x=$\frac{π}{12}$对称 |
3.寒假期间,很多同学都喜欢参加“迎春花市摆档口”的社会实践活动,下表是今年某个档口某种精品的销售数据.
已知摊位租金900元/档,售余精品可以以进货价退回厂家.
(1)画出表中10个销售数据的茎叶图,并求出这组数据的中位数;
明年花市期间甲、乙两位同学想合租一个摊位销售同样的精品,其中甲、乙分别承包白天、晚上的精品销售,承包时间段内销售所获利润归承包者所有.如果其它条件不变,以今年的数据为依据,甲、乙两位同学应如何分担租金才较为合理?
| 日期 | 2月14日 | 2月15日 | 2月16日 | 2月17日 | 2月18日 | |
| 销售量(件) | 白天 | 35 | 32 | 43 | 39 | 51 |
| 晚上 | 46 | 42 | 50 | 52 | 60 | |
(1)画出表中10个销售数据的茎叶图,并求出这组数据的中位数;
明年花市期间甲、乙两位同学想合租一个摊位销售同样的精品,其中甲、乙分别承包白天、晚上的精品销售,承包时间段内销售所获利润归承包者所有.如果其它条件不变,以今年的数据为依据,甲、乙两位同学应如何分担租金才较为合理?
 一个几何体的俯视图如图所示,主视图是底边长为8,高为4的等腰三角形,左视图是底边长为6,高为4的等腰三角形,那么该几何体的全面积是$88+24\sqrt{2}$.
一个几何体的俯视图如图所示,主视图是底边长为8,高为4的等腰三角形,左视图是底边长为6,高为4的等腰三角形,那么该几何体的全面积是$88+24\sqrt{2}$. 如图,已知MA为⊙O的切线,A为切点,△ABC是⊙O的内接三角形,MB交AC于D,交⊙O于E,若MA=MD,∠ABC=60°,ME=1,MB=9,则DC=4.
如图,已知MA为⊙O的切线,A为切点,△ABC是⊙O的内接三角形,MB交AC于D,交⊙O于E,若MA=MD,∠ABC=60°,ME=1,MB=9,则DC=4.