题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,若
,若![]() ,
, ![]() 时,有
时,有![]() 成立.
成立.
(1)判断![]() 在
在![]() 上的单调性,并证明;
上的单调性,并证明;
(2)解不等式![]() ;
;
(3)若![]() 对所有
对所有![]() 的恒成立,求实数
的恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]() (3)
(3)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)根据条件赋值得![]() ,根据奇函数性质得
,根据奇函数性质得![]() ,再根据单调性定义得减函数,(2)利用单调性化简得
,再根据单调性定义得减函数,(2)利用单调性化简得![]() ,结合定义区间得
,结合定义区间得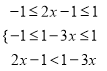 ,解方程组得结果,(3)即
,解方程组得结果,(3)即![]() ,再根据单调性得
,再根据单调性得![]() ,化简得关于a恒成立的不等式,根据一次函数
,化简得关于a恒成立的不等式,根据一次函数![]() 图像得
图像得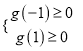 ,解得实数
,解得实数![]() 的取值范围.
的取值范围.
试题解析:证明:(1)![]() 在
在![]() 上是减函数
上是减函数
任取![]() 且
且![]() ,则
,则![]() ,
,
![]() 为奇函数
为奇函数
![]()
![]()
![]()
由题知![]() ,
, ![]()
![]() ,即
,即![]()
![]() 在
在![]() 上单调递减
上单调递减
![]() 在
在![]() 上单调递减
上单调递减
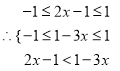
解得不等式的解集为![]()
(3)![]() ,
, ![]() 在
在![]() 上单调递减
上单调递减
![]() 在
在![]() 上,
上, ![]()
问题转化为![]() ,即
,即![]() ,对任意的
,对任意的![]() 恒成立
恒成立
令![]() ,即
,即![]() ,对任意
,对任意![]() 恒成立
恒成立
则由题知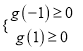 ,解得
,解得![]() 或
或![]() 或
或![]()

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
【题目】某地区某中草药材的销售量与年份有关,下表是近五年的部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
销售量(吨) | 114 | 115 | 116 | 116 | 114 |
(1)利用所给数据求年销售量![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)利用(1)中所求出的直线方程预测该地2018年的中草药的销售量.
参考公式: 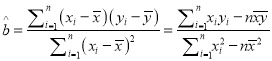 ,
, ![]() .
.