题目内容
(本题满分15分)
已知函数 ,
, 是
是 的导函数(
的导函数( 为自然对数的底数)
为自然对数的底数)
(Ⅰ)解关于 的不等式:
的不等式: ;
;
(Ⅱ)若 有两个极值点
有两个极值点 ,求实数
,求实数 的取值范围.
的取值范围.
(Ⅰ)当 时,无解;当
时,无解;当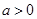 时,解集为
时,解集为 ;当
;当 时,解集为
时,解集为 ;(Ⅱ)
;(Ⅱ) 。
。
解析试题分析:解:(Ⅰ) …………………………2分
…………………………2分 …………………………4分
…………………………4分
当 时,无解; …………………………5分
时,无解; …………………………5分
当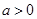 时,解集为
时,解集为 ; …………………………6分
; …………………………6分
当 时,解集为
时,解集为 …………………………7分
…………………………7分
(Ⅱ)方法一:若 有两个极值点
有两个极值点 ,则
,则 是方程
是方程 的两个根
的两个根 ,显然
,显然 ,得:
,得: ……………………………9分
……………………………9分
令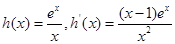 , …………………………11分
, …………………………11分
若 时,
时, 单调递减且
单调递减且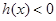 , …………………………12分
, …………………………12分
若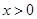 时,当
时,当 时,
时,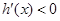 ,
, 在
在 上递减,
上递减,
当 时,
时, ,
, 在
在 上递增,
上递增, ……14分
……14分
要使 有两个极值点,需满足
有两个极值点,需满足 在
在 上有两个不同解,
上有两个不同解,
得: ,即:
,即: ……………………15分
……………………15分
法二:设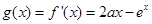 ,
,
则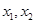 是方程
是方程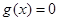 的两个根,则
的两个根,则 , …………………………9分
, …………………………9分
若 时,
时, 恒成立,
恒成立, 单调递减,方程
单调递减,方程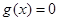 不可能有两个根……11分
不可能有两个根……11分
若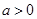 时,由
时,由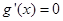 ,得
,得 ,
,
当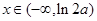 时,
时,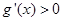 ,
, 单调递增,
单调递增,
当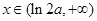 时,
时, 
 单调递减 …………………………13分
单调递减 …………………………13分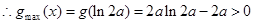 ,得
,得 …………………………15分
…………………………15分
考点:一元二次含参不等式的解法。利用导数研究函数的单调性和极值。
点评:(1)解一元二次含参不等式的主要思想是分类讨论,常讨论的有二次项系数、两根的大小和判别式∆;(2)第二问方法一的关键是把问题转化为“ 有两个不同解”,根据构造函数来求。
有两个不同解”,根据构造函数来求。

 在(-∞,+∞)上是增函数.
在(-∞,+∞)上是增函数. ,设曲线y=
,设曲线y= 在与x轴交点处的切线为y=4x-12,
在与x轴交点处的切线为y=4x-12,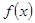 为
为
 ,求函数g(x)在[0,m]上的最大值。
,求函数g(x)在[0,m]上的最大值。 ,若对一切
,若对一切 ,不等式
,不等式 恒成立,求实数t的取值范围
恒成立,求实数t的取值范围 .
. ,
, 在
在 恒成立(其中
恒成立(其中 表示
表示 的导函数),求
的导函数),求 的最大值;
的最大值; 在
在 上有且仅有一个实根,求
上有且仅有一个实根,求 的取值范围.
的取值范围.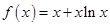 .
. 的图像在点
的图像在点 处的切线方程;
处的切线方程;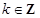 ,且
,且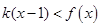 对任意
对任意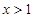 恒成立,求
恒成立,求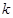 的最大值;
的最大值; .
. 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论; 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值; .
.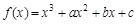 ,过曲线
,过曲线 上的点
上的点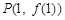 的切线方程为
的切线方程为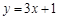
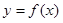 在
在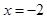 时有极值,求
时有极值,求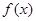 的表达式;
的表达式;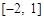 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.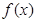


 ,
, 的值;
的值; 的最小值。
的最小值。 )
)
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。 ,曲线
,曲线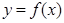 过点
过点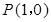 ,且在点
,且在点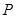 处的切线斜率为2.
处的切线斜率为2.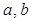 的值;
的值;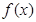 的极值点;
的极值点;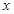 ,不等式
,不等式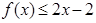 是否恒成立,若成立,请证明;若不成立,请说明理由。
是否恒成立,若成立,请证明;若不成立,请说明理由。