题目内容
16.设实数x?y满足约束条件$\left\{\begin{array}{l}x+y≤10\\ x-y≤2\\ x≥4\end{array}\right.$,则z=2x+3y的最大值为26.分析 作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.
解答 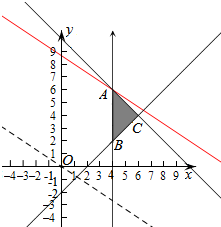 解:作出不等式对应的平面区域(阴影部分),
解:作出不等式对应的平面区域(阴影部分),
由z=2x+3y,得y=$-\frac{2}{3}x+\frac{z}{3}$,
平移直线y=$-\frac{2}{3}x+\frac{z}{3}$,由图象可知当直线y=$-\frac{2}{3}x+\frac{z}{3}$经过点A时,直线y=$-\frac{2}{3}x+\frac{z}{3}$的截距最大,此时z最大.
由$\left\{\begin{array}{l}{x=4}\\{x+y=10}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$,
即A(4,6).
此时z的最大值为z=2×4+3×6=26,
故答案为:26
点评 本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
相关题目
6.设函数f(x)=x2-xlnx+2.
(1)求函数g(x)=f′(x)的极值;
(2)若存在区间[a,b)⊆[$\frac{1}{2}$,+∞),使[a,b]上的值域是[ka,kb],求k的取值范围.
(1)求函数g(x)=f′(x)的极值;
(2)若存在区间[a,b)⊆[$\frac{1}{2}$,+∞),使[a,b]上的值域是[ka,kb],求k的取值范围.
8.执行如图所示的程序框图,则输出的S等于( )

| A. | 19 | B. | 42 | C. | 47 | D. | 89 |
5.已知复数Z满足$\frac{2+4i}{z}$=1-i(i为虚数单位),则复数z=( )
| A. | -1+3i | B. | -1+2i | C. | 1-3i | D. | 1-2i |
6.数列{an}{中,已知a1=1,a2=2,an+1=an+an+2(n∈N+),则a7=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
 如图,在△ABC中,∠B=$\frac{π}{3}$,点D在BC上,cos∠ADC=$\frac{1}{7}$,则cos∠BAD=$\frac{13}{14}$.
如图,在△ABC中,∠B=$\frac{π}{3}$,点D在BC上,cos∠ADC=$\frac{1}{7}$,则cos∠BAD=$\frac{13}{14}$.