题目内容
(本题12分)已知函数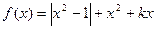 .
.
(1)若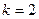 ,求函数
,求函数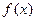 的零点;
的零点;
(2)若关于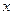 的方程
的方程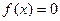 在
在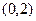 上有2个不同的解
上有2个不同的解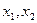 ,求
,求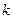 的取值范围,并证明
的取值范围,并证明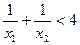 .
.
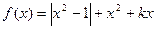 .
.(1)若
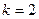 ,求函数
,求函数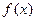 的零点;
的零点;(2)若关于
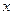 的方程
的方程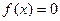 在
在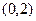 上有2个不同的解
上有2个不同的解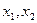 ,求
,求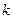 的取值范围,并证明
的取值范围,并证明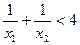 .
.(1)
(2)略

(2)略
解:(1) , …………1分
, …………1分
若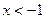 或
或 ,令
,令 ,得
,得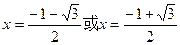 (舍去)
(舍去)
若 ,令
,令 ,得
,得 ,
,
综上,函数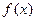 的零点为
的零点为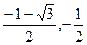 . ………………………………4分
. ………………………………4分
(2) , ……………………………………1分
, ……………………………………1分
因为方程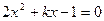 在
在 上至多有1个实根,方程
上至多有1个实根,方程 ,在
,在 上至多有一个实根,结合已知,可得方程
上至多有一个实根,结合已知,可得方程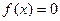 在
在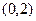 上的两个解
上的两个解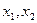 中的1个在
中的1个在 ,1个在
,1个在 。不妨设
。不妨设 ,
, ,
,
法一:设
数形结合可分析出 ,解得
,解得 , ……………………3分
, ……………………3分
 ,
,
 ,
, ,
,
令 ,
, 在
在 上递增,
上递增,
当 时,
时, 。因为
。因为 ,所以
,所以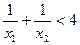 。 …………4分
。 …………4分
 法二:由
法二:由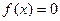 ,可知
,可知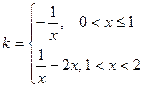 ,
,
作出 的图像。
的图像。
可得 。 ……………………………………………………………3分
。 ……………………………………………………………3分
且 ,故
,故 。 ………………………………4分
。 ………………………………4分
 , …………1分
, …………1分若
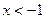 或
或 ,令
,令 ,得
,得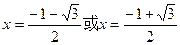 (舍去)
(舍去)若
 ,令
,令 ,得
,得 ,
,综上,函数
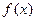 的零点为
的零点为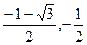 . ………………………………4分
. ………………………………4分(2)
 , ……………………………………1分
, ……………………………………1分因为方程
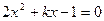 在
在 上至多有1个实根,方程
上至多有1个实根,方程 ,在
,在 上至多有一个实根,结合已知,可得方程
上至多有一个实根,结合已知,可得方程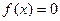 在
在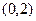 上的两个解
上的两个解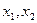 中的1个在
中的1个在 ,1个在
,1个在 。不妨设
。不妨设 ,
, ,
,法一:设

数形结合可分析出
 ,解得
,解得 , ……………………3分
, ……………………3分 ,
, ,
, ,
,令
 ,
, 在
在 上递增,
上递增,当
 时,
时, 。因为
。因为 ,所以
,所以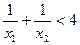 。 …………4分
。 …………4分 法二:由
法二:由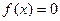 ,可知
,可知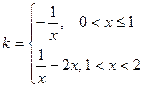 ,
,作出
 的图像。
的图像。可得
 。 ……………………………………………………………3分
。 ……………………………………………………………3分且
 ,故
,故 。 ………………………………4分
。 ………………………………4分
练习册系列答案
相关题目
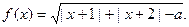
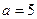 时,求函数
时,求函数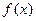 的定义域;
的定义域;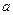 的取值范围.
的取值范围.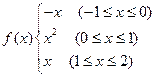
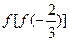 的值;
的值;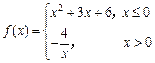 ,若
,若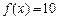 ,则x = ___________
,则x = ___________ ( )
( ) 在区间
在区间 上单调递减,
上单调递减, ,则不等式
,则不等式 的解集为( )
的解集为( )



 ,若
,若 ,则
,则 。
。 ,则
,则 的值为
的值为
 9
9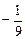
 的定义域分别为
的定义域分别为 ,且
,且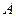 是
是 的真子集.若对任意的
的真子集.若对任意的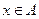 ,都有
,都有 ,则称
,则称 为
为 在
在 ,若
,若 为
为 在
在 上的一个“延拓函数”,且
上的一个“延拓函数”,且


