题目内容
20.某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁珊每米的造价40元,两侧墙砌砖,每米造价45元,顶部每平方米造价20元.(1)设铁珊长为x米,一堵砖墙为y米,求函数y=f(x)的解析式;
(2)要使仓库地面的面积最大,正面铁栅的长度应为多长.
分析 (1)长为x米,宽为y米,则40x+90y+20xy=3200,可得函数y=f(x)的解析式;
(2)由40x+90y≥120$\sqrt{xy}$,得$\sqrt{xy}$的取值范围,即S=xy的取值范围;由40x=90y,且xy=100,解得x,y的值即可.
解答 解:(1)由题意,知:40x+2y×45+20xy=3200,
所以y=$\frac{320-4x}{9+2x}$(0<x<80);
(2)因为40x+90y≥120$\sqrt{xy}$(当且仅当40x=90y时取“=”),
所以:3200≥120$\sqrt{xy}$+20xy,
所以,0<$\sqrt{xy}$≤10;
所以,S=xy≤100.
当40x=90y时,S取最大值,又xy=100,
所以x=15,y=$\frac{20}{3}$,
所以,此时正面铁栅应设计为15米.
点评 本题考查了长方体模型的应用,在求面积S=xy最值时,利用基本不等式是关键.

练习册系列答案
相关题目
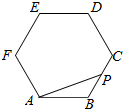 如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].
如图所示:点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动,其中AB=4,则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8,24].