Question

若函数y=f（x）的导函数图象如图所示，则下列判断正确的是（　　）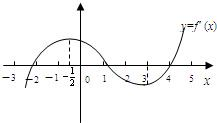

• A、函数f（x）在区间（-3，-

  1

  2

  ）上单调递增
• B、函数f（x）在区间（-

  1

  2

  ，3）上单调递减
• C、函数f（x）在区间（4，5）上单调递增
• D、当x=3时，f（x）有极小值

Answer 1

分析：根据导函数的图象可知：当-2＜x＜1或x＞4时，导函数大于0，得到f（x）为增函数；当x＜-2或1＜x＜4时，函数f（x）是减函数．
且函数的极值点可能在-2，1，4取，所以C正确．

解答：解：由y=f（x）的导函数图象可知：当-2＜x＜1或x＞4时，f′（x）＞0，函数f（x）为增函数；
当x＜-2或1＜x＜4时，f′（x）＜0，函数f（x）为减函数，所以A、B错，
又因为f′（x）=0时，x可以取-2，1，4所以函数f（x）的极值点可能为f（-2），f（1），f（4），所以D错
故选C

点评：考查学生利用数形结合的数学思想解决实际问题的能力，会利用导数研究函数的单调性．