题目内容
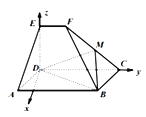
【题目】如图所示,平面CDEF⊥平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,ED⊥CD,AB=3EF=3,ED=a,AD![]() .
.
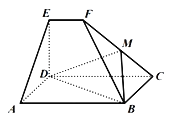
(1)求证:AD⊥BF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求![]() 的值;
的值;
(3)若a=1,求二面角D﹣BC﹣F的余弦值.
【答案】(1)证明见解析;(2)![]() (3)
(3)![]()
【解析】
(1)建立空间直角坐标系,求出直线AD及直线BF的方向向量,利用两向量的数量积为0,即可得证;
(2)设![]() ,根据题设数据,求出平面BDN的一个法向量,以及直线AE的方向向量,利用AE∥平面BDM,建立关于λ的方程,解出即可;
,根据题设数据,求出平面BDN的一个法向量,以及直线AE的方向向量,利用AE∥平面BDM,建立关于λ的方程,解出即可;
(3)求出平面BCF及平面BCD的法向量,利用向量的夹角公式即可得解.
解:(1)∵平面CDEF⊥平面ABCD,ED⊥CD,
∴ED⊥平面ABCD,
如图,以D为原点,DC所在直线为y轴,过点D垂直于DC的直线为x轴,建立空间直角坐标系,
∵∠DAB=45°,AB=3EF=3,![]() ,
,
∴A(1,﹣1,0),B(1,2,0),C(0,3,0),E(0,0,a),F(0,1,a),
∴![]() ,
,
∴![]() ,
,
∴AD⊥EF;
(2)设![]() ,则
,则![]() ,
,
设平面BDM的法向量为![]() ,则
,则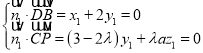 ,
,
取x1=2,则![]() ,
,
若AE∥平面BDM,则![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴线段CF上存在一点M,满足AE∥平面BDM,此时![]() ;
;
(3)设平面BCF的法向量为![]() ,则
,则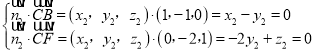 ,
,
取x2=1,则![]() ,
,
又平面BCD的一个法向量为![]() ,
,
∴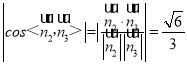 ,
,
由图可知,二面角D﹣BC﹣F为锐角,故二面角D﹣BC﹣F的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目