题目内容
3.求值:${2^{2{{log}_2}3+1}}+({log_{\sqrt{3}}}2-{log_9}8)•{log_2}\sqrt{3}$=$\frac{73}{4}$.分析 利用对数的运算性质、换底公式即可得出.
解答 解:原式=${2}^{lo{g}_{2}({3}^{2}×2)}$+$lo{g}_{\sqrt{3}}2$$•lo{g}_{2}\sqrt{3}$-$\frac{3}{2lo{g}_{2}3}$$•\frac{1}{2}lo{g}_{2}3$
=18+1-$\frac{3}{4}$
=$\frac{73}{4}$.
故答案为:$\frac{73}{4}$.
点评 本题考查了对数的运算性质、换底公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
8.一个算法的程序框图所图所示,则该程序输出的结果为( )
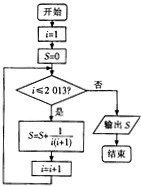

| A. | $\frac{2012}{2013}$ | B. | $\frac{2013}{2014}$ | C. | $\frac{1}{2013}$ | D. | $\frac{1}{2014}$ |
15.已知函数y=sin2x,则函数的周期为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
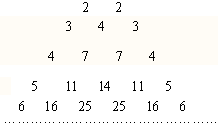 如图,它满足(1)第n行首尾两数均为n,
如图,它满足(1)第n行首尾两数均为n,