题目内容
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)A.(选修4-5 不等式选讲)
若任意实数x使m≥|x+2|-|5-x|恒成立,则实数m的取值范围是
[7,+∞)
[7,+∞)
;B.(选修4-1 几何证明选讲)
如图:EB、EC是⊙O的两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,则∠A的度数是
99°
99°
;C.(选修4-4坐标系与参数方程)
极坐标系下,直线ρcos(θ-
| π |
| 4 |
| 2 |
| 2 |
1
1
.分析:A.构造函数y=|x+2|-|5-x|,根据绝对值的几何意义,我们易得到函数的值域,根据不等式m≥|x+2|-|5-x|恒成立,则ymax≤k,我们可以构造关于m的不等式,进而得到m的取值范围.
B.根据切线长定理得EC=EB,则∠ECB=∠EBC=67°,再根结合内接四边形的对角互补得∠A=∠ECB+∠DCF=67°+32°=99°.
C.把极坐标方程化为直角坐标方程,求出圆心到直线的距离,将此距离和圆的半径作对比,得出结论.
B.根据切线长定理得EC=EB,则∠ECB=∠EBC=67°,再根结合内接四边形的对角互补得∠A=∠ECB+∠DCF=67°+32°=99°.
C.把极坐标方程化为直角坐标方程,求出圆心到直线的距离,将此距离和圆的半径作对比,得出结论.
解答:解:A:令y=|x+2|-|5-x|,
则y∈[-7,7]
若不等式m≥|x+2|-|5-x|恒成立,
则ymax≤k即k≥7.
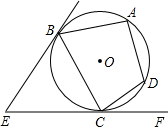 B:∵EB、EC是⊙O的切线,
B:∵EB、EC是⊙O的切线,
∴EB=EC,
又∵∠E=46°,
∴∠ECB=∠EBC=67°,
∴∠BCD=180°-(∠BCE+∠DCF)=180°-99°=81°;
∵四边形ADCB内接于⊙O,
∴∠A+∠BCD=180°,
∴∠A=180°-81°=99°.
C:直线ρcos(θ-
)=
即
ρcosθ+
ρsinθ=
,化为直角坐标方程为 x+y-2=0,
圆ρ=
即 x2+y2=4,圆心到直线的距离等于
=
=
(半径),
故直线和圆相切,故直线和圆有一个交点.
故答案为:[7,+∞);99°; 1.
则y∈[-7,7]
若不等式m≥|x+2|-|5-x|恒成立,
则ymax≤k即k≥7.
 B:∵EB、EC是⊙O的切线,
B:∵EB、EC是⊙O的切线,∴EB=EC,
又∵∠E=46°,
∴∠ECB=∠EBC=67°,
∴∠BCD=180°-(∠BCE+∠DCF)=180°-99°=81°;
∵四边形ADCB内接于⊙O,
∴∠A+∠BCD=180°,
∴∠A=180°-81°=99°.
C:直线ρcos(θ-
| π |
| 4 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
圆ρ=
| 2 |
| |0+0-2| | ||
|
| 2 |
| 2 |
故直线和圆相切,故直线和圆有一个交点.
故答案为:[7,+∞);99°; 1.
点评:A题考查的知识点是绝对值不等式,其中熟练熟练绝对值的几何意义,并分析出绝对值函数的值域是解答此类问题的关系,本题也可以用零点分段法,将构造的函数表示为分段函数,然后求出值域,但过程较为复杂.
B题综合考查了切线长定理、圆内接四边形的性质和等腰三角形的性质以及三角形的内角和定理等知识.
C题考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,求出圆心到直线的距离,是解题的关键.
B题综合考查了切线长定理、圆内接四边形的性质和等腰三角形的性质以及三角形的内角和定理等知识.
C题考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,求出圆心到直线的距离,是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)