题目内容
若f(x)的定义域为[a,b],值域为[a,b](a<b),则称函数f(x)是[a,b]上的“四维光军”函数.
①设g(x)= x2-x+
x2-x+ 是[1,b]上的“四维光军”函数,求常数b的值;
是[1,b]上的“四维光军”函数,求常数b的值;
②问是否存在常数a,b(a>-2),使函数h(x)=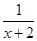 是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
①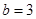 ; ②不存在,详见解析
; ②不存在,详见解析
解析试题分析:①根据信息找到b所满足的等式即可求出b的值,一定要先判断函数在闭区间上的单调性;②先假设存在题目要求的常数,根据“四维光军”函数的特性去找到此常数能得到的结论,推出矛盾即可说明这样的常数是不存在的,这是一种逆向思维的题目,首先假设存在,由存在得出矛盾,则可知存在不成立.
试题解析:①由已知得 ,其对称轴为
,其对称轴为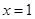 ,区间
,区间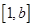 在对称轴的右边,
在对称轴的右边,
所以函数在区间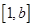 上是单调递增的, 3分
上是单调递增的, 3分
由“四维光军”函数的定义可知,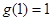 ,
,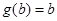 即
即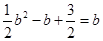 ,又因为
,又因为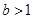 ,解得
,解得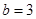 ; 6分
; 6分
②假如函数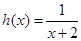 在区间
在区间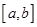
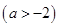 上是“四维光军”函数, 7分
上是“四维光军”函数, 7分
因为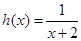 在区间
在区间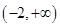 是单调递减函数,则有
是单调递减函数,则有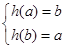 , 10分
, 10分
即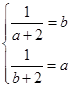 ,解得
,解得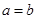 ,这与已知矛盾. 12分
,这与已知矛盾. 12分
考点:函数单调性的应用,函数的图形和性质的应用.

练习册系列答案
相关题目
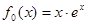 ,
,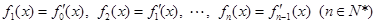 .
.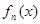 的表达式(不需证明);
的表达式(不需证明);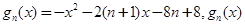 的最大值为
的最大值为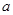 ,
,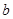 ,求
,求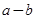 的最小值.
的最小值.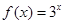 ,
,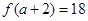 ,
,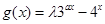 的定义域为
的定义域为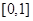
 的值;
的值;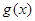 在区间
在区间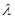 的取值范围。
的取值范围。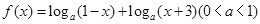 .
. 的定义域 ;
的定义域 ;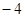 ,求实数
,求实数 的值.
的值. 小时的收费为
小时的收费为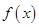 元
元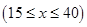 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动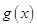 元
元 .设某商品标价为
.设某商品标价为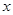 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为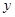 .
. 时,
时,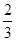 ?
?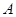 、
、 ,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)
,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)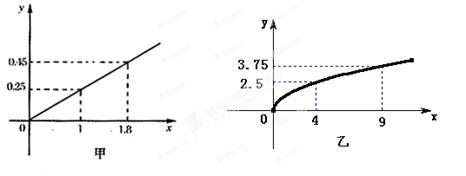
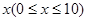 万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.
万元投资A项目, 10-x万元投资B项目.h(x)表示投资A项目所得利润与投资B项目所得利润之和.求h(x)的最大值,并指出x为何值时,h(x)取得最大值.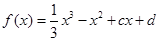
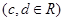 ,其图象为曲线
,其图象为曲线 ,点
,点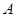 为曲线
为曲线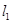 与曲线
与曲线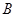 ,在点
,在点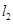 .
.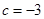 时,求函数
时,求函数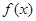 的单调区间;
的单调区间;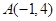 时,
时,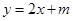 ,求实数
,求实数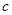 和
和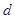 的值;
的值;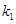 、
、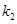 ,试问:是否存在常数
,试问:是否存在常数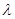 ,使得
,使得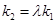 ?若存在,求出
?若存在,求出