题目内容
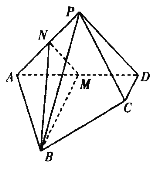
【题目】把半椭圆![]() (
(![]() )与圆弧
)与圆弧![]() (
(![]() )合成的曲线称作“曲圆”,其中
)合成的曲线称作“曲圆”,其中![]() 为
为![]() 的右焦点,如图所示,
的右焦点,如图所示,![]() 、
、![]() 、
、![]() 、
、![]() 分别是“曲圆”与
分别是“曲圆”与![]() 轴、
轴、![]() 轴的交点,已知
轴的交点,已知![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线交“曲圆”于
的直线交“曲圆”于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 轴的上方).
轴的上方).
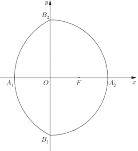
(1)求半椭圆![]() 和圆弧
和圆弧![]() 的方程;
的方程;
(2)当点![]() 、
、![]() 分别在第一、第三象限时,求△
分别在第一、第三象限时,求△![]() 的周长
的周长![]() 的取值范围;
的取值范围;
(3)若射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交“曲圆”于点
交“曲圆”于点![]() ,请用
,请用![]() 表示
表示![]() 、
、![]() 两点的坐标,并求△
两点的坐标,并求△![]() 的面积的最小值.
的面积的最小值.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)易得![]() ,
,![]() ,则
,则![]() ,即可得到结果;
,即可得到结果;
(2)得到周长为![]() ,根据
,根据![]() 范围解得即可;
范围解得即可;
(3)设![]() ,
,![]() ,可知,
,可知,
![]() ,代入椭圆方程解出
,代入椭圆方程解出![]() ,
,![]() ,再根据公式求面积即可
,再根据公式求面积即可
(1)易得![]() ,
,![]() ,则
,则![]()
椭圆![]() :
:![]()
圆弧![]() :
:![]()
(2)由(1)可知![]() 为
为![]() ,
,![]()
![]() 点
点![]() 、
、![]() 分别在第一、第三象限,
分别在第一、第三象限,![]()
![]() ,
,
此时![]() 为腰长为2的等腰三角形,
为腰长为2的等腰三角形,![]() ,
,
![]() 的周长
的周长![]()
![]()
![]() ,
,
![]()
(3)设![]() ,
,![]() ,
,
由题意得,![]()
即![]()
当![]() 时,
时,![]()
①当![]() 时,将点
时,将点![]() 坐标代入
坐标代入![]() 中得,
中得,![]() ,解得
,解得![]() 或
或![]() (舍),可得
(舍),可得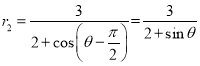
![]()
令![]() ,则
,则![]()
当![]() 时,即
时,即![]() 时,
时,![]()
![]()
②当![]() 时,
时,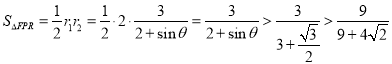
![]()
综上, △![]() 的面积的最小值为
的面积的最小值为![]()

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
【题目】某公司对4月份员工的奖金情况统计如下:
奖金(单位:元) | 8000 | 5000 | 4000 | 2000 | 1000 | 800 | 700 | 600 | 500 |
员工(单位:人) | 1 | 2 | 4 | 6 | 12 | 8 | 20 | 5 | 2 |
根据上表中的数据,可得该公司4月份员工的奖金:①中位数为800元;②平均数为1373元;③众数为700元,其中判断正确的个数为( )
A.0B.1C.2D.3